如图,在 中, , ,动点 从点 出发以 的速度沿 匀速运动,同时动点 从点 出发以 的速度沿 匀速运动,当点 到达点 时,点 、 同时停止运动,设运动时间为 .
(1)当 为何值时,点 在线段 的垂直平分线上?
(2)是否存在某一时刻 ,使 是以 为腰的等腰三角形?若存在,求出 的值;若不存在,请说明理由;
(3)以 为边,往 方向作正方形 ,设四边形 的面积为 ,求 关于 的函数关系式.

如图,在等边△ABC中,AD⊥BC于点D,一个直径与AD相等的圆与BC相切于点E,与AB相切于点F,连接EF。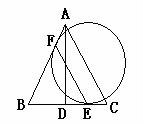
判断EF与AC的位置关系(不必说明理由);
如图,过E作BC的垂线,交圆于G,连接AC,判断四边形ADEG的形状,并说明理由。
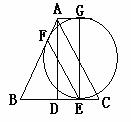
确定圆心O的位置,并说明理由。
探究下表中的奥妙,填空并完成下列题目
| 一元二次方程 |
两个根 |
二次三项式因式分解 |
 |
 |
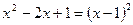 |
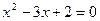 |
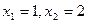 |
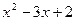 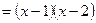 |
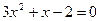 |
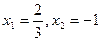 |
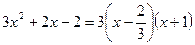 |
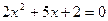 |
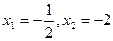 |
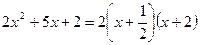 |
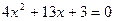 |
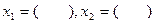 |
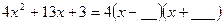 |
如果一元二次方程
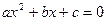 (
(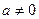 )有解为
)有解为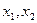 ,请你把二次三项式
,请你把二次三项式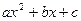 因式分解。
因式分解。利用上面的结论,把二次三项式
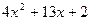 因式分解。
因式分解。
如图,⊙I为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE为⊙I的切线,
求△ADE的周长。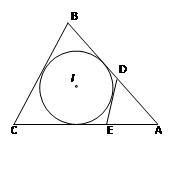
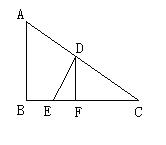
如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.小岛D和小岛F相距多少海里?
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
“一方有难,八方支援”.四川汶川大地震牵动着全国人民的心,我市某医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援汶川.若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果;
求恰好选中医生甲和护士A的概率.