已知:如图, 是 的直径, ,点 , 是 上两点,连接 , , ,弦 平分 , ,过点 作 交 的延长线于点 ,垂足为点 .
(1)求扇形 的面积(结果保留 ;
(2)求证: 是 的切线.

(本小题满分10分)
如图,点P、Q分别是边长为4cm的等边∆ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,
(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)何时∆PBQ是直角三角形?
(3)如图,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;

(本小题满分8分)
学生小明、小华到某电脑销售公司参加社会实践活动,了解到2010年该公司经销的甲、己两种品牌电脑在第一季度三个月(即一、二、三月份)的销售数量情况.小明用直方图表示甲品牌电脑在第一季度每个月的销售量的分布情况,见图;小华用扇形统计图表示乙品牌电脑每个月的销售量与该品牌电脑在第一季度的销售总量的比例分布情况,见图.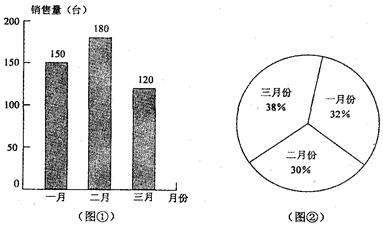
根据上述信息,回答下列问题:
(1)这三个月中,甲品牌电脑在哪个月的销售量最大?▲月份;
(2)已知该公司这三个月中销售乙品牌电脑的总数量比销售甲品牌电脑的总数量多50台,求乙品牌电脑在二月份共销售了多少台?
(3)若乙品牌电脑一月份比甲品牌电脑一月份多销售42台,那么三月份乙品牌电脑比甲品牌电脑多销售(少销售)多少台?
(本小题满分8分)
已知正比例函数 (a<0)与反比例函数
(a<0)与反比例函数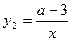 的图象有两个公共点,其中一个公共点的纵坐标为4.
的图象有两个公共点,其中一个公共点的纵坐标为4.
(1)求这两个函数的解析式;
(2)在坐标系中画出它们的图象(可不列表);
(3)利用图像直接写出当x取何值时, .
.
(本小题满分6分)
如图,CD切⊙O于点D,连结OC,交⊙O
于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半
径为10,sin∠COD= .
.
求:(1)弦AB的长;
(2)CD的长;
(本小题满分6分)
在下面三小题中任选其中两小题完成