如图,抛物线 与 轴交于点 和点 (点 在原点的左侧,点 在原点的右侧),与 轴交于点 , .
(1)求该抛物线的函数解析式.
(2)如图1,连接 ,点 是直线 上方抛物线上的点,连接 , . 交 于点 ,当 时,求点 的坐标.
(3)如图2,点 的坐标为 ,点 是抛物线上的点,连接 , , 形成的 中,是否存在点 ,使 或 等于 ?若存在,请直接写出符合条件的点 的坐标;若不存在,请说明理由.

如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
(1)求证:BE=DF;
(2)求证:AF∥CE.
已知x=2是关于x的一元二次方程x2+3x+m-2=0的一个根.
(1)求m的值及方程的另一个根;
(2)若7-x≥1+m(x-3),求x的取值范围.
已知⊙O及⊙O外一点P,过点P作出⊙O的一条切线(只有圆规和三角板这两种工具).以下是甲、乙两同学的作业:
甲:①连接OP,作OP的垂直平分线l,交OP于点A;
②以点A为圆心、OA为半径画弧、交⊙O于点M;
③作直线PM,则直线PM即为所求(如图1).
乙:①让直角三角板的一条直角边始终经过点P;
②调整直角三角板的位置,让它的另一条直角边过圆心O,直角顶点落在⊙O上,记这时直角顶点的位置为点M;
③作直线PM,则直线PM即为所求(如图2).
对于两人的作业,下列说法正确的是()
| A.甲对,乙不对 | B.甲不对,乙对 | C.两人都对 | D.两人都不对 |
如图,在矩形ABCD中,AD=8,AB=6,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P,Q的运动过程中,以PQ为边作正方形PQEF,使它与矩形ABCD在BC的同侧,点P,Q同时出发,当点P返回点M时停止运动,点Q也随之停止,设点P,Q运动的时间是t秒(t>0)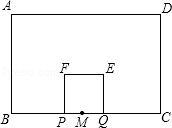
(1)用含t的代数式表示线段BQ的长;
(2)设正方形PQEF与矩形ABCD重叠部分的面积为S,求S与t之间的函数关系式;
(3)连接AC,当正方形PQEF与△ADC重叠部分为三角形时,直接写出t的取值范围.
某企业生产的一批产品上市后30天内全部售完,调查发现,国内市场的日销售量为y1(吨)与时间t(t为整数,单位:天)的关系如图1所示的抛物线的一部分,而国外市场的日销售量y2(吨)与时间t,t为整数,单位:天)的关系如图2所示.
(1)求y1与时间t的函数关系式及自变量t的取值范围,并写出y2与t的函数关系式及自变量t的取值范围;
(2)设国内、国外市场的日销售总量为y吨,直接写出y与时间t的函数关系式,当销售第几天时,国内、外市场的日销售总量最早达到75吨?
(3)判断上市第几天国内、国外市场的日销售总量y最大,并求出此时的最大值.