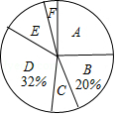
某校为了解学生最喜欢的球类运动情况，随机选取该校部分学生进行调查，要求每名学生只写一类最喜欢的球类运动．以下是根据调查结果绘制的统计图表的一部分．
类别 |
|
|
|
|
|
|
类型 |
足球 |
羽毛球 |
乒乓球 |
篮球 |
排球 |
其他 |
人数 |
10 |
4 |
6 |
2 |
根据以上信息，解答下列问题：
（1）被调查的学生中，最喜欢乒乓球的有 人，最喜欢篮球的学生数占被调查总人数的百分比为 ；
（2）被调查学生的总数为 人，其中，最喜欢篮球的有 人，最喜欢足球的学生数占被调查总人数的百分比为 ；
（3）该校共有450名学生，根据调查结果，估计该校最喜欢排球的学生数．
已知，在平面直角坐标系中，点P（0，2），以P为圆心，OP为半径的半圆与y轴的另一个交点是C，一次函数
（m为实数）的图象为直线l，l分别交x轴，y轴于A，B两点，如图1．
B点坐标是（用含m的代数式表示），∠ABO=°
若点N是直线AB与半圆CO的一个公共点（两个公共点时，N为右侧一点），过点N作⊙P的切线交x轴于点E，如图2．
①是否存在这样的m的值，使得△EBN是直角三角形。若存在，求出m的值；若不存在，请说明理由．
②当
=
时，求m的值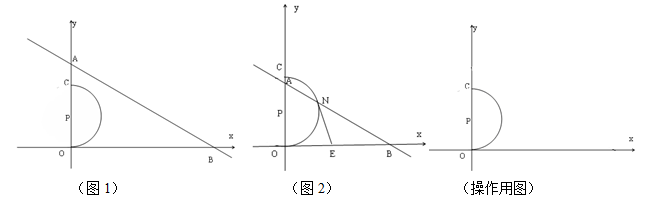
水池中有水20m3，12：00时同时打开两个每分钟出水量相等且不变的出水口，12:06时王师傅打开一个每分钟进水量不变的进水口，同时关闭一个出水口，12:14时再关闭另一个出水口，12:20时水池中有水56m3，王师傅的具体记录如下表．设从12:00时起经过tmin池中有水ym3，右图中折线ABCD表示y关于t的函数图象．
| 时间 |
池中有水（m3） |
| 12:00 |
20 |
| 12:04 |
12 |
| 12:06 |
a |
| 12:14 |
b |
| 12:20 |
56 |
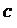
（1）每个出水口每分钟出水m3，表格中a＝；
（2）求进水口每分钟的进水量和b的值；
（3）在整个过程中t为何值时，水池有水16m3？
如图，一次函数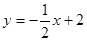
分别交y轴、x轴于A、B两点，抛物线
过A、B两点．
（1）求这个抛物线的解析式；
（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？
阅读下面材料：
小红遇到这样一个问题：如图1，在四边形
中，
，
，
，
，求
的长．
小红发现，延长
与
相交于点
，通过构造Rt△
，经过推理和计算能够使问题得到解决（如图2）．
（1）请回答：的长为．
（2）参考小红思考问题的方法，解决问题：
如图3，在四边形中，
，
，
，
，求
和
的长．
如图，在□ABCD中，点E是DC的中点，连接AE，并延长交BC的延长线于点F．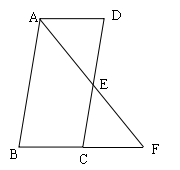
（1）求证：△ADE和△CEF的面积相等
（2）若AB=2AD，试说明AF恰好是∠BAD的平分线