某商场销售一种小商品,每件进货价为190元,调查发现,当销售价为210元时,平均每天能销售8件;当销售价每降低2元时,平均每天就能多销售4件,设每件小商品降价 元,平均每天销售 件.
(1)求 与 之间的函数关系式;
(2)商场要想使这种小商品平均每天的销售利润达到280元,求每件小商品的销售价应定为多少元?
(3)设每天的销售总利润为 元,求 与 之间的函数关系式;每件小商品降价多少元时,每天的总利润最大?最大利润是多少?
解方程组: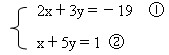
解方程组:
如图,AB∥CD,EF分别交AB、CD于M、N ∠EMB=50°,MG平分∠BMF,MG交CD于G.求∠1的度数.
根据提示填空(或填上每步推理的理由)
已知:如图,∠1=∠2、∠3=∠4,求证:∠5=∠A.
证明:∵∠1=∠2.(已知)
∠3=∠4,(已知)
又∵∠2=∠3( )
∴∠1=∠4.( )
∴_______//_______( )
∴∠5=∠A( )
根据提示填空(或填上每步推理的理由)
如图,∠1=∠2,∠3=108°.求∠4的度数。
解:∵∠1=∠2(已知)
∴AB∥CD()
∴∠3+∠4=180°()
∵∠3=108°(已知)
∴∠4=180°-108°=72°