在运动会前夕，育红中学都会购买篮球、足球作为奖品．若购买10个篮球和15个足球共花费3000元，且购买一个篮球比购买一个足球多花50元．
（1）求购买一个篮球，一个足球各需多少元？
（2）今年学校计划购买这种篮球和足球共10个，恰逢商场在搞促销活动，篮球打九折，足球打八五折，若此次购买两种球的总费用不超过1050元，则最多可购买多少个篮球？
已知：如图，四边形ABCD中，∠B＝
，AB＝3，BC＝4，CD＝12，AD＝13求四边形ABCD的面积。
如果一个三角形的三边长分别为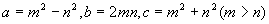
，则这三角形是直角三角形。
已知a，b，c为△ABC的三边且满足a2c2－b2c2=a4－b4，试判断△ABC的形状．小明同学是这样解答的．
解：∵a2c2－b2c2=a4－b4， ∴
∴
．订正：∴ △ABC是直角三角形 ．
横线与问号是老师给他的批注，老师还写了如下评语：“你的解题思路很清晰，但解题过程中出现了错误，相信你再思考一下，一定能写出完整的解题过程．”请你帮助小明订正此题，好吗？
如图１，一架长4米的梯子AB斜靠在与地面OM垂直的墙壁ON上，梯子与地面的倾斜角α为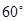
．（1）求AO与BO的长；（2）若梯子顶端A沿NO下滑，同时底端B沿OM向右滑行.如图2，设A点下滑到C点，B点向右滑行到D点，并且AC:BD=2:3，试计算梯子顶端A沿NO下滑多少米?
阅读下列题目的解题过程：已知a、b、c为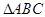
的三边，且满足
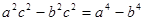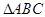，试判断的形状．
解：
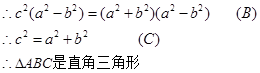
问：（1）上述解题过程，从哪一步开始出现错误？请写出该步的代号：
（2）错误的原因为：
（3）本题正确的结论为：