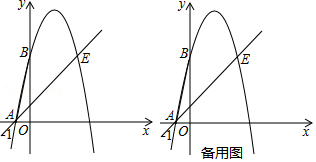
如图,抛物线 经过点 ,点 ,与 轴交于点 ,连接 .
(1)求该抛物线的解析式;
(2)将 绕点 旋转,点 的对应点为点 .
①当点 落在直线 上时,求点 的坐标和 的面积;
②当点 到直线 的距离为 时,过点 作直线 的平行线与抛物线相交,请直接写出交点的坐标.
往直径为680mm的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽AB=600mm,求油的最大深度.
如图,点O、A、B的坐标分别为(0,0)(4,2)(3,0),将△OAB绕点O按逆时针方向旋转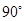 后,得到△OCD.(点A转到点C)
后,得到△OCD.(点A转到点C)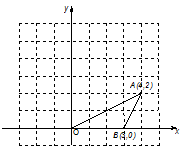
(1)画出△OCD;
(2)C的坐标为;
(3)求A点开始到结束所经过路径的长.
如图,在△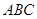 中,∠
中,∠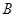 >∠
>∠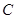 ,
,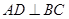 ,
,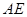 平分∠
平分∠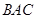 .
.
(1)若∠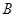 =70°,∠
=70°,∠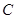 =30°.
=30°.
①求∠ =°;②∠
=°;②∠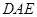 =°.
=°.
(2)探究:小明认为如果只要知道∠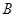 -∠
-∠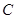 =n°,就能求出∠
=n°,就能求出∠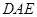 的度数?请你就这个问题展开探究:
的度数?请你就这个问题展开探究:
①实验:填表
∠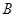 的度数 的度数 |
∠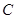 的度数 的度数 |
∠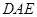 的度数 的度数 |
| 70° |
30° |
(此格不需填写) |
| 65° |
25° |
|
| 50° |
20° |
|
| 80° |
56° |
②结论:当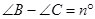 时,试用含
时,试用含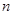 的代数式表示∠
的代数式表示∠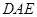 的度数,并写出推导过程;
的度数,并写出推导过程;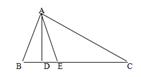
③应用:若∠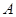 =56°,∠
=56°,∠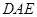 =12°,则∠
=12°,则∠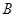 =°
=°
某学校班主任暑假带领该班三好学生去旅游,甲旅行社说:“如果教师买全票一张,其余学生享受半价优惠” ;乙旅行社说:“教师在内全部按票价的6折优惠” ;若全票价格是240元/张.
(1)如果有10名学生,应选择哪个旅行社,并说出理由;
(2)当学生人数是多少时,两家旅行社收费一样多.
如图,已知AE∥BD,∠1=3∠2,∠2=25°,求∠C的度数.