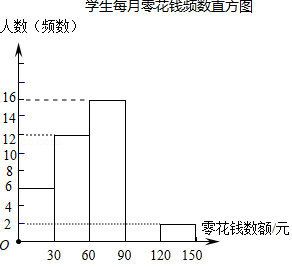
为了解同学们每月零花钱数额，校园小记者随机调查了本校部分学生-优题课

题文

为了解同学们每月零花钱数额，校园小记者随机调查了本校部分学生，并根据调查结果绘制出如下不完整的统计图表：

请根据以上图表，解答下列问题：

零花钱数额 $x /$ 元	人数（频数）	频率
$0 ⩽ x < 30$	6	0.15
$30 ⩽ x < 60$	12	0.30
$60 ⩽ x < 90$	16	0.40
$90 ⩽ x < 120$	$b$	0.10
$120 ⩽ x < 150$	2	$a$

（1）这次被调查的人数共有　　人， $a =$ 　　．

（2）计算并补全频数分布直方图；

（3）请估计该校1500名学生中每月零花钱数额低于90元的人数．

科目数学题型解答题难度中等

知识点：用样本估计总体频数（率）分布表频数（率）分布直方图

登录免费查看答案和解析

相关试题

（1）计算：
（2）先化简，再求值：，请代入一个你喜欢的值并进行计算．

（本小题满分11分）已知关于x的函数y=m－x－（m－1）.
（1）m=__________时，y=m－x－（m－1）是一次函数；
（2）求证：对任何实数m，y=m－x－（m－1）的图像与都有公共点；
（3）若是关于的二次函数y=m－x－（m－1）的图像与x有两个不同的公共点A、B （点A在点B左边），图像顶点为C，且△ABC是等腰直角三角形，求m的值；
（4）是否存在这样的点P，使得对任何实数m，y=m－x－（m－1）的图像都经过P点？若存在，求出所有P的坐标；若不存在，请说明理由.

（本小题满分9分）如图，在矩形ABCD中，E是CD边上一动点，设DE＝x，作AF⊥AE交CB的延长线于点F．

（1）当点E不与点C，D重合时，求证：△ADE∽△ABF；
（2）连接EF，M为EF的中点，AB＝4，AD＝2，当点E从D运动到C的过程中
①点M经过的路径是（）

②求点M经过的路径的长；
③连接BM，直接写出BM的长度的最小值．

（本小题满分8分）某技工培训中心有钳工20名、车工30名. 现将这50名技工中的15人派往A地工作，35人派往B地工作，两地技工的工资情况如下表：

工种属地	钳工	车工
地	1800（元/月）	1600（元/月）
地	1600（元/月）	1200（元/月）

设派往A地x名钳工时，这50名技工的月工资总额为y元.
（1）派往B地___________名钳工，派往B地___________名车工；
（2）求y关于x的函数关系式；
（3）若A地钳工的月工资总额不小于B地钳工的月工资总额，派往A地多少名钳工，可使这50名技工的月工资总额最高？

（本小题满分7分）如图，已知半径为2的⊙O与直线相切于点A，点P是直径AB左侧半圆上的动点，过点P作直线的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC的长为x（2＜x＜4）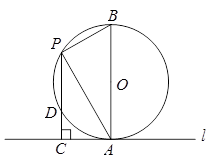

（1）当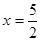时，求弦PA、PB的长度；
（2）当x为何值时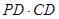，的值最大？最大值是多少？

试卷网试题网古诗词网作文网范文网