我省中小学积极开展综合实践活动,某校准备组织开展四项综合实践活动:“ .我是非遗小传人, .学做家常餐, .爱心义卖行动, .找个岗位去体验”.为了解学生最喜爱哪项综合实践活动,随机抽取部分学生进行问卷调查(每位学生只能选择一项),将调查结果绘制成下面两幅不完整的统计图,请结合图中提供的信息回答下列问题:
(1)本次一共调查了 名学生,在扇形统计图中, 的值是 ;
(2)补全条形统计图;
(3)若该校共有1200名学生,估计最喜爱 和 项目的学生一共有多少名?
(4)现有最喜爱 , , , 活动项目的学生各一人,学校要从这四人中随机选取两人交流活动体会,请用列表或画树状图的方法求出恰好选取最喜爱 和 项目的两位学生的概率.

一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)小明认为口袋中共有三种颜色的球,所以从袋中任意摸出一球,摸到红球、白球或黄球的概率都是 ,你认为对吗?请你用列表或画树状图的方法说明理由.
,你认为对吗?请你用列表或画树状图的方法说明理由.
(本题满分8分)先化简,再求值: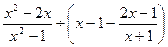 ,选一个你喜欢的实数x代入求值.
,选一个你喜欢的实数x代入求值.
(本题6分)已知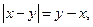 且
且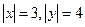 ,试求
,试求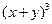 的值
的值
简答题(共2题,每小题3分,共6分)
(1)根据生活经验,对代数式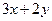 作出解释.
作出解释.
(2) 两个有理数的和是负数,那么这两个数一定都是负数,这种说法对吗?如果不对,请举例说明?
计算及化简: