如图1,在平面直角坐标系中,一次函数 的图象与 轴交于点 ,与 轴交于 点,抛物线 经过 , 两点,在第一象限的抛物线上取一点 ,过点 作 轴于点 ,交直线 于点 .
(1)求抛物线的函数表达式;
(2)是否存在点 ,使得 和 相似?若存在,请求出点 的坐标,若不存在,请说明理由;
(3)如图2, 是第一象限内抛物线上的动点(不与点 重合),点 是线段 上的动点.连接 , ,当四边形 是平行四边形且周长最大时,请直接写出点 的坐标.

生活中,有人喜欢把传送的便条折成 形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为
形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为 ,宽为
,宽为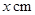 ,分别回答下列问题:
,分别回答下列问题: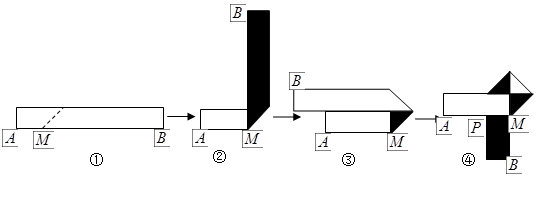
(1)为了保证能折成图④的形状(即纸条两端均超出点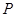 ),试求
),试求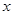 的取值范围.
的取值范围.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点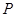 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点
的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点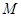 与点
与点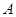 的距离(用
的距离(用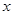 表示)
表示)
如图已知∠AOB,OA=OB,点E在OB上,四边形AEBF是矩形,请你只用无刻度的直尺画出∠AOB的角平分线,并请证明你所画的是正确的。(保留作图痕迹)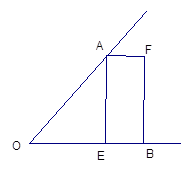
某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投5个球,下图记录的是这两名同学5次投篮中所投中的个数.
| 姓名 |
平均数 |
众数 |
方差 |
| 王亮 |
7 |
||
| 李刚 |
7 |
2.8 |
(1)请你根据图中的数据,填写右表.
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.
观察下列各式: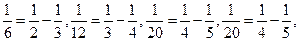
(1)由此可以推断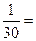 。
。
(2)请用上面的规律解方程: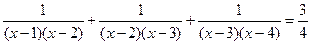
解下列不等式组: