如图1，在四边形 中，如果对角线 和 相交并且相等，那么我们把这样的四边形称为等角线四边形．
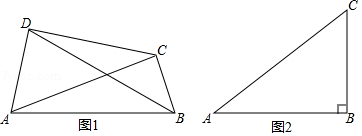
（1）①在“平行四边形、矩形、菱形”中， 一定是等角线四边形（填写图形名称）；
②若 、 、 、 分别是等角线四边形 四边 、 、 、 的中点，当对角线 、 还要满足 时，四边形 是正方形．
（2）如图2，已知 中， ， ， ， 为平面内一点．
①若四边形 是等角线四边形，且 ，则四边形 的面积是 ；
②设点 是以 为圆心，1为半径的圆上的动点，若四边形 是等角线四边形，写出四边形 面积的最大值，并说明理由．
2013年，东营市某楼盘以每平方米6500元的均价对外销售．因为楼盘滞销，房地产开发商为了加快资金周转，决定进行降价促销，经过连续两年下调后，2015年的均价为每平方米5265元．
（1）求平均每年下调的百分率；
（2）假设2016年的均价仍然下调相同的百分率，张强准备购买一套100平方米的住房，他持有现金20万元，可以在银行贷款30万元，张强的愿望能否实现？（房价每平方米按照均价计算）
如图是函数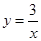
与函数
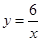在第一象限内的图象，点
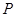是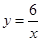的图象上一动点，
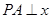轴于点A，交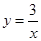的图象于点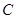
，
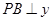轴于点B，交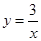的图象于点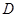
．
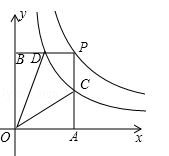
（1）求证：D是BP的中点；
（2）求出四边形ODPC的面积．
已知在△ABC中，∠B=90o，以AB上的一点O为圆心，以OA为半径的圆交AC于点D，交AB于点E．
（1）求证：AC·AD=AB·AE；
（2）如果BD是⊙O的切线，D是切点，E是OB的中点，当BC=2时，求AC的长．
东营市为进一步加强和改进学校体育工作，切实提高学生体质健康水平，决定推进“一校一球队、一级一专项、一人一技能”活动计划．某校决定对学生感兴趣的球类项目（A：足球，B：篮球，C：排球，D：羽毛球，E：乒乓球）进行问卷调查，学生可根据自己的喜好选修一门，李老师对某班全班同学的选课情况进行统计后，制成了两幅不完整的统计图（如图）．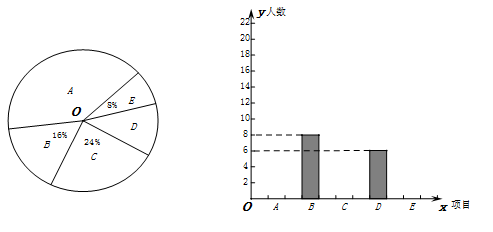
（1）将统计图补充完整；
（2）求出该班学生人数；
（3）若该校共有学生3500名，请估计有多少人选修足球？
（4）该班班委5人中，1人选修篮球，3人选修足球，1人选修排球，李老师要从这5人中任选2人了解他们对体育选修课的看法，请你用列表或画树状图的方法，求选出的2人恰好1人选修篮球，1人选修足球的概率．
如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
（1）请画出△ABC向左平移5个单位长度后得到的△A1B1C1；
（2）请画出△ABC关于原点对称的△A2B2C2；
（3）在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标．