初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 |
男生(人数) |
女生(人数) |
机器人 |
7 |
9 |
打印 |
|
4 |
航模 |
2 |
2 |
其他 |
5 |
|
根据以上信息解决下列问题:
(1) , ;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.

把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12cm,DC=14cm,把三角板DCE绕点C逆时针旋转15°得到△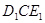 (如图2).这时AB与
(如图2).这时AB与 相交于点O,与
相交于点O,与 相交于点F.
相交于点F.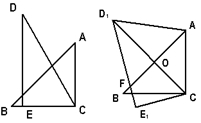
(1)填空:∠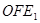 =°;
=°;
(2)请求出△ 的内切圆半径;
的内切圆半径;
(3)把△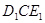 绕着点C逆时针再旋转
绕着点C逆时针再旋转 度(
度( )得△
)得△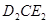 ,若△
,若△ 为等腰三角形,求
为等腰三角形,求 的度数(精确到0.1°).
的度数(精确到0.1°).
如图是无锡某比赛场馆的平面图,根据距离比赛场地的远近和视角的不同,将观赛场地划分成A、B、C三个不同的票价区.其中与场地边缘MN的视角大于或等于45°,并且距场地边缘MN的距离不超过15米的区域划分为A票区,B票区(如图1所示),剩下的为C票区.
(1)请你利用尺规作图,在观赛场地中,作出A票区所在的区域(只要求作出图形,保留作图痕迹,不要求写作法);
(2)如果每个座位所占的平均面积是1.2平方米,请估算A票区有多少个座位;
(3)为提高B区观众的观赛效果,举办方将B区用两个大型的支柱AP、AC撑起一定的角度,其横截面如图2所示.若AB=10米,∠B=30°,∠CPA=∠CAD=75°,求CP的长度.(结果保留根号)
(1)大桥中学初三学生对迎新文艺汇演的满意程度进行测评,评定分A、B、C、D四个等第,为了解评定情况,小明随机调查初三30名学生的学号及他们的满意度等第,结果如下:
| 学号 |
3002 |
3015 |
3039 |
3068 |
3075 |
3115 |
3132 |
3145 |
3156 |
3178 |
| 等第 |
A |
B |
C |
B |
A |
A |
C |
B |
A |
D |
| 学号 |
3209 |
3233 |
3251 |
3260 |
3279 |
3295 |
3313 |
3336 |
3341 |
3387 |
| 等第 |
B |
B |
A |
C |
A |
B |
B |
A |
A |
B |
| 学号 |
3399 |
3416 |
3452 |
3488 |
3493 |
3499 |
3501 |
3538 |
3567 |
3583 |
| 等第 |
A |
A |
B |
B |
A |
B |
C |
C |
B |
B |
注:等第A,B,C,D分别代表满意、较满意、一般、不满意.
①请在下面给出的图中画出这30名学生对文艺汇演满意程度等第的频数条形统计图,并计算其中等第达到较满意以上(含较满意)的频率;
②已知初三学生学号是从3001开始,按由小到大顺序排列的连续整数,请你计算这30名学生学号的中位数,并运用中位数的知识来估计这次初三学生的满意度等第达到较满意以上(含较满意)的人数;
(2)迎新文艺汇演组委会准备邀请所有参与表演的学生去嬉戏谷游玩,由于项目较多,准备上午先从 A.雷神之怒、B.龙行天下、C.撕裂星空、D.云之秘境中随机选择三个项目,下午再从E.天际骇客、F.激流勇进、G.魔兽天途中随机选择二个项目游玩,
①请用列举法或树形图说明当天学生们符合上述条件的所有可能的选择方式.(用字母表示)
②在①的选择方式中,求学生恰好上午选中A雷神之怒,同时下午选中G天际骇客这两个项目的概率.
如图,等腰三角形ABC中,AC=BC=3,AB=4.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.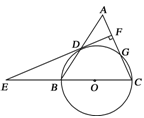
(1)求证:直线EF是⊙O的切线;
(2)连接BG,求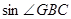 的值.
的值.
关于x的一元二次方程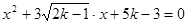 ,问:是否存在整数k使方程有两个不相等的实数根,若存在,请求出k的值并求出此时方程的两个实数根;若不存在,试说明理由.
,问:是否存在整数k使方程有两个不相等的实数根,若存在,请求出k的值并求出此时方程的两个实数根;若不存在,试说明理由.