在矩形 中, , ,动点 从点 出发,以每秒1个单位的速度,沿 向点 移动;同时点 从点 出发,仍以每秒1个单位的速度,沿 向点 移动,连接 , , .若两个点同时运动的时间为 秒 ,解答下列问题:
(1)设 的面积为 ,用含 的函数关系式表示 ;当 为何值时, 有最大值?并求出最小值;
(2)是否存在 的值,使得 ?试说明理由.

.(2011福建龙岩,20, 10分)如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F。求证:AE=CF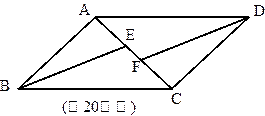
解不等式组: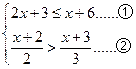 ,并把解集在数轴上表示出来。
,并把解集在数轴上表示出来。
先化简,再求值: ,其中 .(结果精确到0.01)
观察下面的点阵图和相应的等式,探究其中的规律:
(1)在④和⑤后面的横线上分别写出相应的等式;
(2)试用含有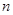 的式子表示这一规律;
的式子表示这一规律;
(3)根据上面算式的规律,请计算:1+3+5+…+99。
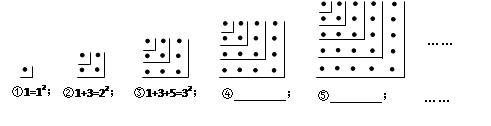 |
已知A、B在数轴上分别表示 、
、
(1)对照数轴填写下表:
 |
6 |
—6 |
—6 |
—6 |
2 |
—1.5 |
 |
4 |
0 |
4 |
—4 |
—10 |
—1.5 |
| A、B两点的距离 |
(2)若A、B两点间的距离记为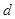 ,试问
,试问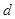 和
和 、
、 有何数量关系?
有何数量关系?
(3)在数轴上标出所有符合条件的整数点P,使它到10和—10的距离之和为20,并求所有这些整数的和。
(4)若点C表示的数为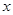 ,当点
,当点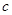 在什么位置时,
在什么位置时,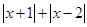 取得的值最小?
取得的值最小?