如图1,抛物线 与 轴交于点 , ,与 轴交于点 ,顶点为 ,直线 交 轴于点 .
(1)求抛物线的解析式.
(2)如图2,将 沿直线 平移得到 .
①当点 落在抛物线上时,求点 的坐标.
②在 移动过程中,存在点 使 为直角三角形,请直接写出所有符合条件的点 的坐标.

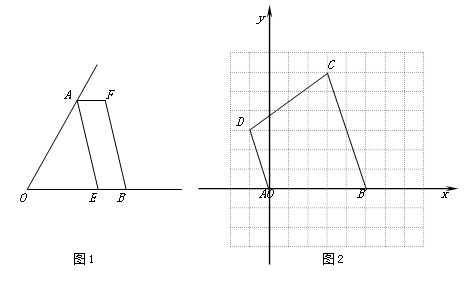
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,请你只用无刻度的直尺在图中画出∠AOB的平分线.(保留作图痕迹,不要求写作法)
(2)如图2,在10×10的正方形网格中,点A(0,0)、B(5,0)、C(3,6)、D(-1,3),
①依次连结A、B、C、D四点得到四边形ABCD,四边形ABCD的形状是▲ .
②在x轴上找一点P,使得△PCD的周长最短(直接画出图形,不要求写作法);
此时,点P的坐标为▲ ,最短周长为▲ .
 |
在中央电视台第2套《购物街》栏目中,有一个精彩刺激的游戏――幸运大转盘,其规则如下:
①游戏工具是一个可绕轴心自由转动的圆形转盘,转盘按圆心角均匀划分为20等分,并在其边缘标记5、10、15、…、100共20个5的整数倍数,游戏时,选手可旋转转盘,待转盘停止时,指针所指的数即为本次游戏的得分;
②每个选手在旋转一次转盘后可视得分情况选择是否再旋转转盘一次,若只旋转一次,则以该次得分为本轮游戏的得分,若旋转两次则以两次得分之和为本轮游戏的得分;
③若某选手游戏得分超过100分,则称为“爆掉”,该选手本轮游戏裁定为“输”,在得分不超过100分的情况下,分数高者裁定为“赢”;
④遇到相同得分的情况,相同得分的选手重新游戏,直到分出输赢.
现有甲、乙两位选手进行游戏,请解答以下问题:
(1)甲已旋转转盘一次,得分65分,他选择再旋转一次,求他本轮游戏不被“爆掉”的概率.
(2)若甲一轮游戏最终得分为90分,乙第一次旋转转盘得分为85分,则乙还有可能赢吗?赢的概率是多少?
(3)若甲、乙两人交替进行游戏,现各旋转一次后甲得85分,乙得65分,你认为甲是否应选择旋转第二次?说明你的理由.
某中学九(1)班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.

请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为▲ ;
(2)选择长跑训练的人数占全班人数的百分比是▲ ,该班共有同学▲ 人;
(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25% , 请求出参加训练之前的人均进球数.
已知:如图,AB是⊙O的直径,点C、D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积.
.先化简分式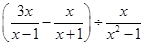 ,再从不等式组
,再从不等式组 的解集中取一个合适的值代入,求原分式的值.
的解集中取一个合适的值代入,求原分式的值.