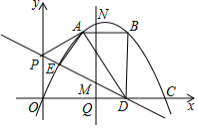
如图,在平面直角坐标系中,抛物线 , 为常数, 经过两点 , ,交 轴正半轴于点 .
(1)求抛物线 的解析式.
(2)过点 作 垂直于 轴,垂足为点 ,连接 , ,将 以 为轴翻折,点 的对应点为 ,直线 交 轴于点 ,请判断点 是否在抛物线上,并说明理由.
(3)在(2)的条件下,点 是线段 (不包含端点)上一动点,过点 垂直于 轴的直线分别交直线 及抛物线于点 , ,连接 ,请探究:是否存在点 ,使 是以 为腰的等腰三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元.商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
如图1,△ABC中,∠ACB=90°,E是AB的中点, ED平分∠BEC交BC于点D,F在DE延长线上且AF=AE.
(1)求证:四边形ACEF是平行四边形;
(2)如图2若四边形ACEF是菱形,连接FC,BF,FC与AB交于点H,连接DH,在不添加任何辅助线的情况下,请直接写出图2中的所有等边三角形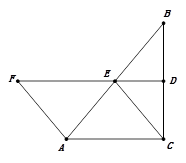
在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是 ,
,
(1)将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF;
(2)将线段AF绕点O旋转180°得到线段MN,点A、F对应点分别是M、N,请画出线段MN,并连结NF,直接写出线段NF的长
先化简,再求代数式 的值,其中
的值,其中 x=
x= ×
× +1
+1
解方程:
(1)x(2x-5)=4x-10(2)2x2-x-1="0"