如图，OF是∠MON的平分线，点A在射线OM上，P，Q是直线-优题课

题文

如图， $OF$ 是 $∠ MON$ 的平分线，点 $A$ 在射线 $OM$ 上， $P$ ， $Q$ 是直线 $ON$ 上的两动点，点 $Q$ 在点 $P$ 的右侧，且 $PQ = OA$ ，作线段 $OQ$ 的垂直平分线，分别交直线 $OF$ 、 $ON$ 于点 $B$ 、点 $C$ ，连接 $AB$ 、 $PB$ ．

（1）如图1，当 $P$ 、 $Q$ 两点都在射线 $ON$ 上时，请直接写出线段 $AB$ 与 $PB$ 的数量关系；

（2）如图2，当 $P$ 、 $Q$ 两点都在射线 $ON$ 的反向延长线上时，线段 $AB$ ， $PB$ 是否还存在（1）中的数量关系？若存在，请写出证明过程；若不存在，请说明理由；

（3）如图3， $∠ MON = 60 °$ ，连接 $AP$ ，设 $\frac{AP}{OQ} = k$ ，当 $P$ 和 $Q$ 两点都在射线 $ON$ 上移动时， $k$ 是否存在最小值？若存在，请直接写出 $k$ 的最小值；若不存在，请说明理由．

科目数学题型解答题难度中等

知识点：相似三角形的判定与性质全等三角形的判定与性质相似形综合题

登录免费查看答案和解析

相关试题

小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查，由调查结果绘制了频数分布直方图，根据图中信息回答下列问题：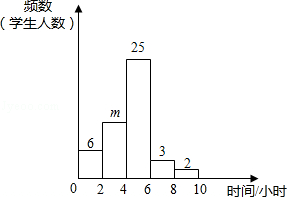

（1）求m的值；
（2）从参加课外活动时间在6～10小时的5名学生中随机选取2人，请你用列表或画树状图的方法，求其中至少有1人课外活动时间在8～10小时的概率．

如图，在平面直角坐标系中，O为原点，一次函数与反比例函数的图象相交于A（2，1）B（－1，－2）两点，与轴相交于点C．

（1）分别求反比例函数和一次函数的解析式（关系式）；
（2）连接OA，求△AOC的面积．

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B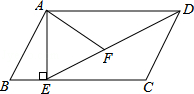

（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求AE的长．

如图，△ABC三个定点坐标分别为A（﹣1，3），B（﹣1，1），C（﹣3，2）．

（1）请画出△ABC关于y轴对称的△A₁B₁C₁；
（2）以原点O为位似中心，将△A₁B₁C₁放大为原来的2倍，得到△A₂B₂C₂，请在第三象限内画出△A₂B₂C₂，并求出S_△A1B1C1：S_△A2B2C2的值．

（1）解方程：，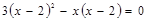
（2）小丽为校合唱队购买某种服装时，商店经理给出了如下优惠条件：如果一次性购买不超过10件，单价为80元；如果一次性购买多于10件，那么每增加1件，购买的所有服装的单价降低2元，但单价不得低于50元．按此优惠条件，小丽一次性购买这种服装付了1200元．请问她购买了多少件这种服装？

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号