如图1,抛物线 与 轴交于点 和 (点 在点 的左侧),与 轴交于点 ,连接 .
(1)求 、 的值;
(2)如图2,点 为抛物线上的一动点,且位于直线 上方,连接 、 .求 面积的最大值;
(3)如图3,点 、 分别为线段 和线段 上的动点,连接 、 ,是否存在这样的点 ,使 为等腰三角形, 为直角三角形同时成立?若存在,求出点 的坐标;若不存在,请说明理由.

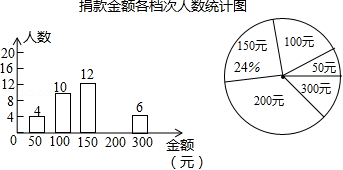
企业举行“爱心一日捐”活动,捐款金额分为五个档次,分别是50元,100元,150元,200元,300元.宣传小组随机抽取部分捐款职工并统计了他们的捐款金额,绘制成两个不完整的统计图,请结合图表中的信息解答下列问题:
(1)宣传小组抽取的捐款人数为 人,请补全条形统计图;
(2)统计的捐款金额的中位数是 元;
(3)在扇形统计图中,求100元所对应扇形的圆心角的度数;
(4)已知该企业共有500人参与本次捐款,请你估计捐款总额大约为多少元?
先化简,再求值: ,其中 满足 .
如图,二次函数 的图象经过点 , , ,直线 与 轴交于点 , 为二次函数图象上任一点.
(1)求这个二次函数的解析式;
(2)若点 在直线 的上方,过 分别作 和 轴的垂线,交直线 于不同的两点 , 在 的左侧),求 周长的最大值;
(3)是否存在点 ,使得 是以 为直角边的直角三角形?如果存在,求点 的坐标;如果不存在,请说明理由.

为迎接“国家卫生城市”复检,某市环卫局准备购买 、 两种型号的垃圾箱,通过市场调研得知:购买3个 型垃圾箱和2个 型垃圾箱共需540元;购买2个 型垃圾箱比购买3个 型垃圾箱少用160元.
(1)每个 型垃圾箱和 型垃圾箱各多少元?
(2)现需要购买 , 两种型号的垃圾箱共300个,分别由甲、乙两人进行安装,要求在12天内完成(两人同时进行安装).已知甲负责 型垃圾箱的安装,每天可以安装15个,乙负责 型垃圾箱的安装,每天可以安装20个,生产厂家表示若购买 型垃圾箱不少于150个时,该型号的产品可以打九折;若购买 型垃圾箱超过150个时,该型号的产品可以打八折,若既能在规定时间内完成任务,费用又最低,应购买 型和 型垃圾箱各多少个?最低费用是多少元?
某体育场看台的坡面 与地面的夹角是 ,看台最高点 到地面的垂直距离 为3.6米,看台正前方有一垂直于地面的旗杆 ,在 点用测角仪测得旗杆的最高点 的仰角为 ,已知测角仪 的高度为1.6米,看台最低点 与旗杆底端 之间的距离为16米( , , 在同一条直线上).
(1)求看台最低点 到最高点 的坡面距离;
(2)一面红旗挂在旗杆上,固定红旗的上下两个挂钩 、 之间的距离为1.2米,下端挂钩 与地面的距离为1米,要求用30秒的时间将红旗升到旗杆的顶端,求红旗升起的平均速度(计算结果保留两位小数) , , , , ,
