(探究证明)
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
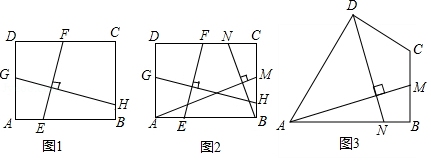
如图1,矩形 中, , 分别交 , 于点 , , 分别交 , 于点 , .求证: ;
(结论应用)
(2)如图2,在满足(1)的条件下,又 ,点 , 分别在边 , 上,若 ,则 的值为 ;
(联系拓展)
(3)如图3,四边形 中, , , , ,点 , 分别在边 , 上,求 的值.
解方程:
如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连结AB.点P从
点B出发,以每秒4个单位长度的速度沿BC方向运动,到点C停止.当点P与B、C
两点不重合时,作PD⊥BC交AB于D,作DE⊥AC于E.F为射线CB上一点,且∠CEF=∠ABC.设
点P的运动时间为x(秒).
(1)用含有x的代数式表示CF的长.
(2)求点F与点B重合时x的值.
(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式.
(4)当x为某个值时,沿PD将以D、E、F、B为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x值.
甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备
后,乙组的工作效率是原来的2倍.两组各自加工零件的数量 (件)与时间
(件)与时间 (时)的函数图
(时)的函数图
象如图所示.
(1)求甲组加工零件的数量y与时间 之间的函数关系式.
之间的函数关系式.
(2)求乙组加工零件总量 的值.
的值.
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?
探究
如图①,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.
应用
以□ABCD的四条边为边,在其形外分别作正方形,如图②,连结EF、GH、IJ、KL.若□ABCD的面积为5,则图中阴影部分四个三角形的面积和为.
如图,平面直角坐标系中,抛物线
交
轴于点
,
为抛物线
上一点,且与点
不重合.连结
,以
,
为邻边作
,
所在直线与
轴交
于点
.设点P的横坐标为
.
(1)点
落在
轴上时
的值.
(3)若点
在
轴下方,则
为何值时,线段
的长取最大值,并求出这个最大值.[参考公式:二次函数
的顶点坐标为
]