夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务．为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元．
（1）设第 天生产空调 台，直接写出 与 之间的函数解析式，并写出自变量 的取值范围．
（2）若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第 天的利润为 元，试求 与 之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少．
已知正方形ABCD的边心距OE=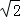
cm，求这个正方形外接圆⊙O的面积．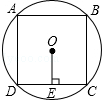
已知A、B两点，求作：过A、B两点的⊙O及⊙O的内接正六边形ABCDEF．（要求用直尺和圆规作图，保留作图痕迹，不必写作法及证明．）
已知：如图1，图形①满足AD=AB，MD=MB，∠A=72°，∠M=144°．图形②与图形①恰好拼成一个菱形（如图2）．记AB的长度为a，BM的长度为b．
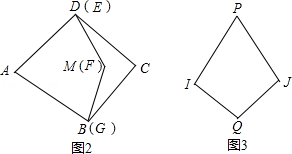
（1）图形①中∠B=°，图形②中∠E=°；
（2）小明有两种纸片各若干张，其中一种纸片的形状及大小与图形①相同，这种纸片称为“风筝一号”；另一种纸片的形状及大小与图形②相同，这种纸片称为“飞镖一号”．
①小明仅用“风筝一号”纸片拼成一个边长为b的正十边形，需要这种纸片张；
②小明若用若干张“风筝一号”纸片和“飞镖一号”纸片拼成一个“大风筝”（如图3），其中∠P=72°，∠Q=144°，且PI=PJ=a+b，IQ=JQ．请你在图3中画出拼接线并保留画图痕迹．（本题中均为无重叠、无缝隙拼接）
如图，在平面直角坐标系中，点P的坐标为（﹣4，0），⊙P的半径为2，将⊙P沿x轴向右平移4个单位长度得⊙P1
（1）画出⊙P1，并直接判断⊙P与⊙P1的位置关系；
（2）设⊙P1与x轴正半轴，y轴正半轴的交点分别为A、B．求劣弧
与弦AB围成的图形的面积（结果保留π）
如图，在梯形ABCD中，AB∥CD，∠BAD=90°，以AD为直径的半圆O与BC相切．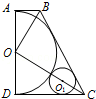
（1）求证：OB⊥OC；
（2）若AD=12，∠BCD=60°，⊙O1与半⊙O外切，并与BC、CD相切，求⊙O1的面积．