某中学九年级数学兴趣小组想测量建筑物 的高度.他们在 处仰望建筑物顶端,测得仰角为 ,再往建筑物的方向前进6米到达 处,测得仰角为 ,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据: , , ,

命题“有两边相等的两个直角三角形全等”是真命题还是假命题?请给出证明.
已知x和y是实数,举例说明下列说法是错误的.
(1)│x+y│=│x│+│y│;(2)若x≤y,则x2≤y2.
判断下列命题的真假,并给出证明.
(1)正比例函数的函数值随着自变量的增大而增大;
(2)有一个角为60°的等腰三角形是等边三角形;
(3)一个角的补角大于这个角;
(4)若一个角的两边分别平行于另一个角的两边,则这两个角相等;
(5)如果n是整数,那么n2+3n+2是偶数.
用反例来证明下列命题是假命题.
(1)若xy=0,则x,y同时为零;(2)两个负数的差一定是负数;
(3)两个锐角的和一定大于直角;(4)任何有理数都有倒数.
在四边形ABCD中,∠A=∠B,∠C=∠ADC.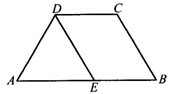
(1)求证:AB∥CD.
(2)若∠ADC-∠A=60°,过点D作DE∥BC交AB于点E.请判断△ADE是哪种特殊三角形,并说明理由.