如图，抛物线yax2bx过A(4,0)，B(1,3)两点，点-优题课

游客

题文

如图，抛物线 $y = a x^{2} + bx$ 过 $A (4, 0)$ ， $B (1, 3)$ 两点，点 $C$ 、 $B$ 关于抛物线的对称轴对称，过点 $B$ 作直线 $BH ⊥ x$ 轴，交 $x$ 轴于点 $H$ ．

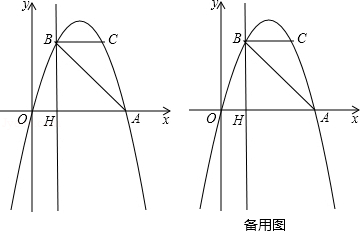
（1）求抛物线的表达式；

（2）直接写出点 $C$ 的坐标，并求出 $ΔABC$ 的面积；

（3）点 $P$ 是抛物线上一动点，且位于第四象限，当 $ΔABP$ 的面积为6时，求出点 $P$ 的坐标；

（4）若点 $M$ 在直线 $BH$ 上运动，点 $N$ 在 $x$ 轴上运动，当以点 $C$ 、 $M$ 、 $N$ 为顶点的三角形为等腰直角三角形时，请直接写出此时 $ΔCMN$ 的面积．

科目数学题型解答题难度较难

知识点：二次函数的性质待定系数法求二次函数解析式二次函数综合题

登录免费查看答案和解析

相关试题

（1）计算： sin60°+|1﹣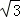|+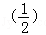^﹣1（2）化简：

面给出的三块正方形纸板的边长都是60cm，请分别按下列要求设计一种剪裁方法，折叠成一个礼品包装盒（纸板的厚度忽略不计）．要求尽可能多地利用纸板，用虚线表示你的设计方案，并把剪裁线用实线标出．
（1）包装礼盒的六个面由六个矩形组成（如图1），请画出对应的设计图．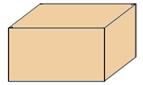

图1
（2）包装礼盒的上盖由四个全等的等腰直角三角形组成（如图2），请画出对应的设计图．

图2
（3）包装礼盒的上盖是双层的，由四个全等的矩形组成（如图3），请画出对应的设计图．

图3

学习了勾股定理的逆定理，我们知道：在一个三角形中，如果两边的平方和等于第三边的平方，那么这个三角形为直角三角形．类似地，我们定义：对于任意的三角形，设其三个内角的度数分别为x°、y°和z°，若满足，则称这个三角形为勾股三角形．
（1）根据“勾股三角形”的定义，请你直接判断命题：“直角三角形是勾股三角形”是真命题还是假命题？
（2）已知某一勾股三角形的三个内角的度数从小到大依次为x°、y°和z°，且xy=2160，求x+y的值；
（3）如图，△ABC内接于⊙O，AB=，AC=1+，BC=2，⊙O的直径BE交AC于点D．
①求证：△ABC是勾股三角形；
②求DE的长．