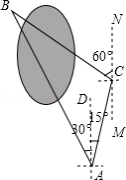
小明要测量公园被湖水隔开的两棵大树 和 之间的距离,他在 处测得大树 在 的北偏西 方向,他从 处出发向北偏东 方向走了200米到达 处,测得大树 在 的北偏西 方向.
(1)求 的度数;
(2)求两棵大树 和 之间的距离(结果精确到1米)(参考数据: , ,
如图,矩形对角线AC,BD相交于点O,∠AOB=60°,AB=4cm,求矩形对角线AC和BC的长.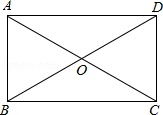
解分式方程: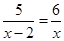 .
.
如图,正三角形ABC内接于⊙O,P是 上的一点,且
上的一点,且 ,
, 交
交 于E,点F是
于E,点F是 延长线上的点,
延长线上的点, ,
, ,
, .
.
(1)求证 ≌
≌ ;
;
(2)求证 ;
;
(3)求 和
和 的长.
的长.
已知关于x的二次函数 的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.
的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.
(1)求k的值;
(2)在(1)的条件下,若反比例函数 的图象与二次函数
的图象与二次函数 的图象从左到右交于Q,R,S三点,且点Q的坐标为(-1,-1),点R(
的图象从左到右交于Q,R,S三点,且点Q的坐标为(-1,-1),点R( ,
, ),S(
),S( ,
, )中的纵坐标
)中的纵坐标 ,
, 分别是一元二次方程
分别是一元二次方程 的解,求四边形AQBS的面积
的解,求四边形AQBS的面积 ;
;
(3)在(1),(2)的条件下,在x轴下方是否存在二次函数 图象上的点P使得
图象上的点P使得 =2
=2 ,若存在,求出点P的坐标;若不存在,请说明理由.
,若存在,求出点P的坐标;若不存在,请说明理由.
直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点
的直线OB交于第三象限的B点,且∠ABO=30°.求: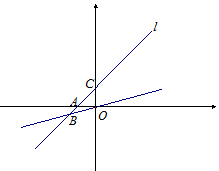
(1)点A、C的坐标;
(2)点B的坐标.