有一个运输队承包了一家公司运送货物的业务,第一次运送 ,派了一辆大卡车和5辆小卡车;第二次运送 ,派了两辆大卡车和11辆小卡车,并且两次派的车都刚好装满.
(1)两种车型的载重量各是多少?
(2)若大卡车运送一次的费用为200元,小卡车运送一次的费用为60元,在第一次运送过程中怎样安排大小车辆,才能使费用最少?(直接写出派车方案)
如图,平行四边形ABCD的对角线AC,BD交于点0,E,F在AC上,G,H在BD上,且AF=CE,BH=DG.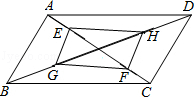
求证:FG∥HE.
已知一次函数的图象过点(3,5)与点(﹣4,﹣9),求这个一次函数的解析式.
如图,已知AC=4,BC=3,BD=12,AD=13,∠ACB=90°,试求阴影部分的面积.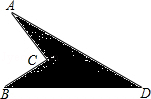
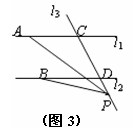
如图,已知直线l1∥l2,直线l3和直线l1、l2交于C、D两点,点P在直线CD上.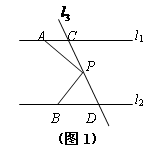
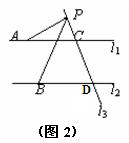
(1)试写出图1中∠APB、∠PAC、∠PBD之间的关系,并说明理由;
(2)如果P点在C、D之间运动时,∠APB,∠PAC,∠PBD之间的关系会发生变化吗?
答: .(填发生或不发生);
(3)若点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2、图3),试分别写出∠APB,∠PAC,∠PBD之间的关系,并说明理由.
为了抓住集安国际枫叶旅游节的商机,某商店决定购进A、B两种旅游纪念品.若购进A种
纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,
需要800元.
(1)求购进A、B两种纪念品每件各需多少元;
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100
件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)
问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?