为了抓住集安国际枫叶旅游节的商机,某商店决定购进A、B两种旅游纪念品.若购进A种
纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,
需要800元.
(1)求购进A、B两种纪念品每件各需多少元;
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100
件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)
问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
如图,⊙O1、⊙O2交于A、B两点,点O1在⊙O2上,两圆的连心线交⊙O1于E、D,交⊙O2于F,交AB于C,请根据图中所给的已知条件(不再标注其他字母, 不再添加任何辅助线),写出两个线段之间的关系式.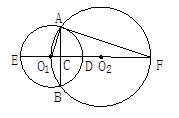
试用10个圆设计一个使各圆都内切的图案.
某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上, 向内放入两个半径为5cm的钢球,测得上面一个钢球顶部高DC=16cm(钢管的轴截面如图所示), 求钢管的内直径AD的长.
|
|
|



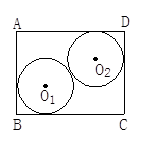
若两圆的圆心距d满足等式│d-4│=3,且两圆的半径是方程x2-7x+12="0" 的两个根,试判断这两圆的位置关系.
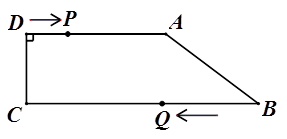
已知梯形 中,
中, ∥
∥ ,
, ,
, ,
, ,
,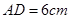 .动点
.动点 从
从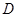 点开始以
点开始以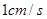 的速度沿线段
的速度沿线段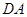 向
向 点运动,动点
点运动,动点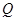 从点
从点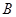 开始以
开始以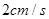 的速度沿线段
的速度沿线段 向
向 点运动.点
点运动.点 、点
、点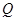 分别从
分别从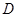 、
、 两点同时出发,当其中一点停止时,另一点也随之停止。设运动时间为
两点同时出发,当其中一点停止时,另一点也随之停止。设运动时间为 .
.
(1)求 的长;
的长;
(2)以 为圆心、
为圆心、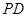 长为半径的
长为半径的 与直线
与直线 相切时,求
相切时,求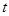 的值;
的值;
(3)是否存在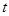 的值,使得以
的值,使得以 为圆心、
为圆心、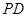 长为半径的
长为半径的 与以
与以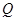 为圆心、
为圆心、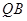 长为半径的
长为半径的 相切?若存在,求出
相切?若存在,求出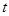 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.