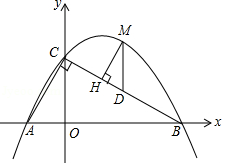
如图,直线 分别与 轴、 轴交于 、 两点,点 在 轴上, ,抛物线 经过 , 两点.
(1)求 、 两点的坐标;
(2)求抛物线的解析式;
(3)点 是直线 上方抛物线上的一点,过点 作 于点 ,作 轴交 于点 ,求 周长的最大值.
如图,在甲、乙两个4×4的方格图中,每个小正方形的边长都为1.
(1)请求出图甲中阴影正方形的面积和边长;
(2)请在图乙中画一个与图甲阴影部分面积不相等的正方形,要求它的边长为无理数,并求出它的边长.
注:答案直接写在图下方的横线上即可.
甲:面积= ;边长= .
乙:边长= .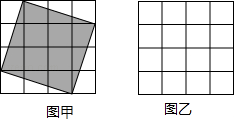
把下列各数填在相应的大括号内:
﹣2,π,0,﹣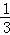 ,﹣0.3,
,﹣0.3,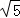 ,1.1010010001…(每两个1之间依次多1个0)
,1.1010010001…(每两个1之间依次多1个0)
整数{ …}
负分数{ …}
无理数{ …}.
当x取什么值时,代数式 与
与 的差等于5.
的差等于5.
小莹用30元钱买了5千克至关苹果和2千克香蕉,找回3元.已知每千克香蕉的售价是每千克苹果售价的2倍,每千克香蕉的售价是多少元?
解下列方程:
(1)3(y+1)=2y﹣1
(2)2(x﹣2)﹣3(4x﹣1)=9(1﹣x)
(3)2[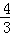 x﹣(
x﹣(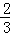 x﹣
x﹣ )]=
)]=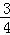 x
x
(4)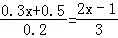 .
.