2018年东营市教育局在全市中小学开展了“情系疏勒书香援疆”捐书活动,200多所学校的师生踊跃参与,向新疆疏勒县中小学共捐赠爱心图书28.5万余本.某学校学生社团对本校九年级学生所捐图书进行统计,根据收集的数据绘制了下面不完整的统计图表.请你根据统计图表中所提供的信息解答下列问题:
图书种类 |
频数(本 |
频率 |
名人传记 |
175 |
|
科普图书 |
|
0.30 |
小说 |
110 |
|
其他 |
65 |
|
(1)求该校九年级共捐书多少本;
(2)统计表中的 , , , ;
(3)若该校共捐书1500本,请估计“科普图书”和“小说”一共多少本;
(4)该社团3名成员各捐书1本,分别是1本“名人传记”,1本“科普图书”,1本“小说”,要从这3人中任选2人为受赠者写一份自己所捐图书的简介,请用列表法或树状图求选出的2人恰好1人捐“名人传记”,1人捐“科普图书”的概率.

解不等式组: .
.
如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,当一点到达终点时,另一点也停止运动.设运动时间为x秒,△PBQ的面积为y(cm2).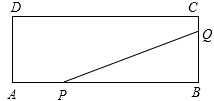
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示: 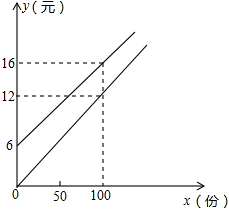
(1)填空:甲种收费的函数关系式是.
乙种收费的函数关系式是.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算?
已知:如图,△ABC中,以AB为直径的⊙O交AC于点D,且D为AC的中点,过D作DE丄CB,垂足为E.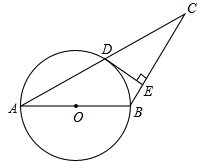
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)已知CD=4,CE=3,求⊙O的半径.
今年我区为绿化行车道,计划购买甲、乙两种树苗共计n棵.设买甲种树苗x棵.有关甲、乙两种树苗的信息如图所示.
(1)当n=500时,
①根据信息填表(用含x代数式表示)
②如果购买甲、乙两种树苗共用25600元,那么甲、乙两种树苗各买了多少棵?
(2)要使这批树苗的成活率不低于92%,且使购买这两种树苗的总费用为26000元,求n的最大值.