如图,在平面直角坐标系中, , , ,点 的坐标为 .抛物线 经过 、 两点.
(1)求抛物线的解析式;
(2)点 是直线 上方抛物线上的一点,过点 作 垂直 轴于点 ,交线段 于点 ,使 .
①求点 的坐标;
②在直线 上是否存在点 ,使 为直角三角形?若存在,求出符合条件的所有点 的坐标;若不存在,请说明理由.

先化简,再求值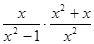 ,其中
,其中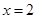 。
。
解不等式组并把解集在数轴上表示出来。
某工程机械厂根据市场需求,计划生产A、B两种型号的大型运输机械共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产此两种型号的大型运输机械,所生产的此两型大型运输机械可全部售出,此两型大型运输机械生产成本和售价如下表:
| 型号 |
A |
B |
| 成本(万元/台) |
200 |
240 |
| 售价(万元/台) |
250 |
300 |
该厂对这两型大型运输机械有哪几种生产方案?
该厂如何生产能获得最大利润?
根据市场调查,每台B型大型运输机械的售价不会改变,每台A型大型运输机械的售价将会提高m万元(m>0),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)
如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.求证:DE是⊙O的切线;
若DE=3,⊙O的半径为5,求BF的长.

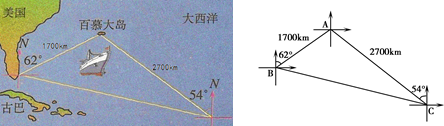
多年来,许多船只、飞机都在大西洋的一个区域内神秘失踪,这个区域被称为百慕大三角.根据图中标出的百慕大三角的位置及相关数据计算:∠BAC的度数;
百慕大三角的面积.(参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)