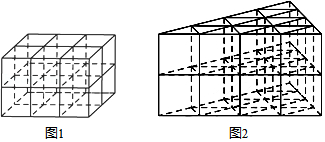
问题提出:用若干相同的一个单位长度的细直木棒,按照如图1方式搭建一个长方体框架,探究所用木棒条数的规律.
问题探究:
我们先从简单的问题开始探究,从中找出解决问题的方法.
探究一
用若干木棒来搭建横长是 ,纵长是 的矩形框架 、 是正整数),需要木棒的条数.
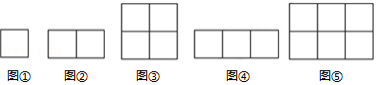
如图①,当 , 时,横放木棒为 条,纵放木棒为 条,共需4条;
如图②,当 , 时,横放木棒为 条,纵放木棒为 条,共需7条;
如图③,当 , 时,横放木棒为 条,纵放木棒为 条,共需12条;
如图④,当 , 时,横放木棒为 条,纵放木棒为 条,共需10条;
如图⑤,当 , 时,横放木棒为 条,纵放木棒为 条,共需17条.
问题(一 :当 , 时,共需木棒 条.
问题(二 :当矩形框架横长是 ,纵长是 时,横放的木棒为 条,
纵放的木棒为 条.
探究二
用若干木棒来搭建横长是 ,纵长是 ,高是 的长方体框架 、 、 是正整数),需要木棒的条数.
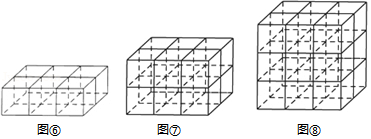
如图⑥,当 , , 时,横放与纵放木棒之和为 条,竖放木棒为 条,共需46条;
如图⑦,当 , , 时,横放与纵放木棒之和为 条,竖放木棒为 条,共需75条;
如图⑧,当 , , 时,横放与纵放木棒之和为 条,竖放木棒为 条,共需104条.
问题(三 :当长方体框架的横长是 ,纵长是 ,高是 时,横放与纵放木棒条数之和为 条,竖放木棒条数为 条.
实际应用:现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是 .
拓展应用:若按照如图2方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒 条.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上两点,经过A、C、B的抛物线的一部分 与经过点A、D、B的抛物线的一部分
与经过点A、D、B的抛物线的一部分 组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,
组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0, ),点M是抛物线
),点M是抛物线 :
: 的顶点.
的顶点.
(1)求A、B两点的坐标.
(2)“蛋线”在第四象限上是否存在一点P,使得 的面积最大?若存在,求出
的面积最大?若存在,求出 面积的最大值;若不存在,请说明理由;
面积的最大值;若不存在,请说明理由;
(3)当 为直角三角形时,直接写出m的值.______
为直角三角形时,直接写出m的值.______
以平面上一点O为直角顶点,分别画出两个直角三角形,记作△AOB和△COD,其中∠ABO=∠DCO=30°.
(1)点E、F、M分别是AC、CD、DB的中点,连接EF和FM.
①如图1,当点D、C分别在AO、BO的延长线上时, =_______;
=_______;
②如图2,将图1中的△AOB绕点O沿顺时针方向旋转 角(
角( ),其他条件不变,判断
),其他条件不变,判断 的值是否发生变化,并对你的结论进行证明;
的值是否发生变化,并对你的结论进行证明;
(2)如图3,若BO= ,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
已知关于x的方程 .
.
(1)当k取何值时,方程有两个实数根;
(2)若二次函数 的图象与
的图象与 轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
(3)若(2)中的抛物线与x轴交于A、B两点,与y轴交于C点.将抛物线向上平移n个单位,使平移后得到的抛物线的顶点落在△ABC的内部(不包括△ABC的边界),写出n的取值范围.
老师要求同学们在图①中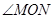 内找一点P,使点P到OM、ON的距离相等.
内找一点P,使点P到OM、ON的距离相等.
小明是这样做的:在OM、ON上分别截取OA=OB,连结AB,取AB中点P,点P即为所求.
请你在图②中的 内找一点P,使点P到OM的距离是到ON距离的2倍.要求:简单叙述做法,并对你的做法给予证明.
内找一点P,使点P到OM的距离是到ON距离的2倍.要求:简单叙述做法,并对你的做法给予证明.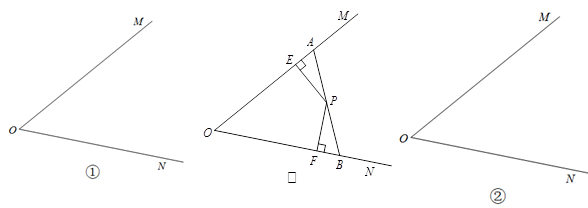
如图,在Rt△ABC中,∠ABO=90°,OB=4,AB=8,且反比例函数 在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若
在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若 ,
,
(1)求反比例函数解析式;
(2)求C点坐标.