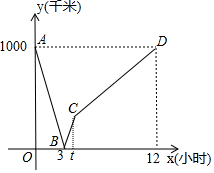
首条贯通丝绸之路经济带的高铁线 宝兰客专进入全线拉通试验阶段．宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义．试运行期间，一列动车从西安开往西宁，一列普通列车从西宁开往西安，两车同时出发，设普通列车行驶的时间为 （小时），两车之间的距离为 （千米），图中的折线表示 与 之间的函数关系，根据图象进行以下探究：
（信息读取）
（1）西宁到西安两地相距 千米，两车出发后 小时相遇；
（2）普通列车到达终点共需 小时，普通列车的速度是 千米 小时．
（解决问题）
（3）求动车的速度；
（4）普通列车行驶 小时后，动车到达终点西宁，求此时普通列车还需行驶多少千米到达西安？
．
；
.
＋2sin45°－
