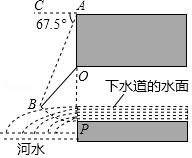
如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中 为下水管道口直径, 为可绕转轴 自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径 , 为检修时阀门开启的位置,且 .
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中 的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达 位置时,在点 处测得俯角 ,若此时点 恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
, , , , , ,
如图,在四边形ABCD中,点E.F.G.H分别为四边形ABCD各边的中点,顺次连接点E.F.G.H,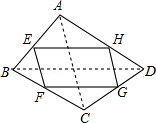
(1)试判断四边形EFGH的形状,并证明你的结论.
(2)如果四边形ABCD是矩形,则四边形EFGH是什么形状?并说明理由.
如图,在正方形ABCD中,点E、F分别在边AB、BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连结DB交CF于点O,延长OB至点G,使OG=OD,连结EG、FG,判断四边形DEGF是否是菱形,并说明理由.
如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
已知:如图,在▱ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.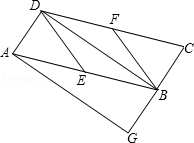
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.