如图,在平面直角坐标系中,菱形 的边 在 轴上,点 坐标 ,点 在 轴正半轴上,且 ,点 从原点 出发,以每秒一个单位长度的速度沿 轴正方向移动,移动时间为 秒,过点 作平行于 轴的直线 ,直线 扫过四边形 的面积为 .
(1)求点 坐标.
(2)求 关于 的函数关系式.
(3)在直线 移动过程中, 上是否存在一点 ,使以 、 、 为顶点的三角形是等腰直角三角形?若存在,直接写出 点的坐标;若不存在,请说明理由.

如图,圈O1与圈O2相交于A、B两点,若AB=O1A=4,O2A=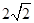 .
.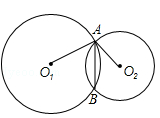
求:(1)∠O1AO2的度数;
(2)O1与O2之间的距离.
如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.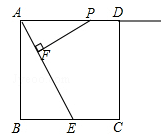
(1)求证:△PFA∽△ABE;
(2)若AP= ,求△PFA的面积.
,求△PFA的面积.
已知抛物线 (
( )经过点(2,
)经过点(2, ).
).
(1)求a的值;
(2)若点A( ,
, ),B(
),B( ,
, )(
)( )都在该抛物线上,试比较
)都在该抛物线上,试比较 与
与 的大小.
的大小.
如图,二次函数 的图象与
的图象与 轴交于
轴交于 ,
, 两点,且与y轴交于点C.
两点,且与y轴交于点C.
(1)求该抛物线的关系式,并判断 的形状;
的形状;
(2)在x轴上方的抛物线上有一点D,且以A、B、C、D四点为顶点的四边形是等腰梯形,请直接写出D点的坐标;
(3)在此抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形是直角梯形?若存在,求出P点的坐标;若不存在,说明理由。
如图,在矩形ABCD中,AB=20cm,BC=4cm,点p从A开始折线A——B——C——D以4cm/秒的 速度 移动,点Q从C开始沿CD边以1cm/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动的时间t(秒)
(1)t为何值时,四边形APQD为矩形.
(2)如图(2),如果⊙P和⊙Q的半径都是2cm,那么t为何值时,⊙P和⊙Q外切?