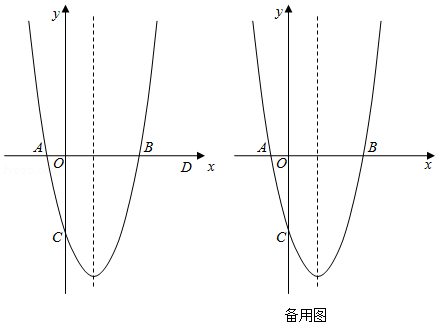
如图,抛物线 的对称轴为直线 ,抛物线与 轴交于点 和点 ,与 轴交于点 ,且点 的坐标为 .
(1)求抛物线的函数表达式;
(2)将抛物线 图象 轴下方部分沿 轴向上翻折,保留抛物线在 轴上的点和 轴上方图象,得到的新图象与直线 恒有四个交点,从左到右四个交点依次记为 , , , .当以 为直径的圆过点 时,求 的值;
(3)在抛物线 上,当 时, 的取值范围是 ,请直接写出 的取值范围.
甲、乙两同学投掷一枚骰子,用字母p、q分别表示两人各投掷一次的点数.
(1)求满足关于x的方程 有实数解的概率.
有实数解的概率.
(2)求(1)中方程有两个相同实数解的概率.
黄冈某地“杜鹃节”期间,某公司70名职工组团前往参观欣赏,旅游景点规定:①门票每人60元,无优惠;②上山游玩可坐景点观光车,观光车有四座和十一座车,四座车每辆60元,十一座车每人10元.公司职工正好坐满每辆车且总费用不超过5000元,问公司租用的四座车和十一座车各多少辆?
如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD =AB·AE,求证:DE是⊙O的切线.
=AB·AE,求证:DE是⊙O的切线.

第20题图
如图是我市某校八年级学生为玉树灾区捐款情况抽样调查的条形图和扇形统计图.
(1)求该样本的容量;
(2)在扇形统计图中,求该样本中捐款15元的人数所占的圆心角度数;
(3)若该校八年级学生有800人,据此样本求八年级捐款总数.
第19题图
如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由。
第18题图