在"新冠"疫情期间，全国人民"众志成城，同心抗疫"，某商家决定将一个月获得的利润全部捐赠给社区用于抗疫．已知商家购进一批产品，成本为10元 件，拟采取线上和线下两种方式进行销售．调查发现，线下的月销量 （单位：件）与线下售价 （单位：元 件， 满足一次函数的关系，部分数据如下表：
（元 件） |
12 |
13 |
14 |
15 |
16 |
（件 |
1200 |
1100 |
1000 |
900 |
800 |
（1）求 与 的函数关系式；
（2）若线上售价始终比线下每件便宜2元，且线上的月销量固定为400件．试问：当 为多少时，线上和线下月利润总和达到最大？并求出此时的最大利润．
某地为了了解当地推进“阳光体育”运动情况，就“中小学每天在校体育活动时间”的问题随机调查了300名中小学生.根据调查结果绘制成的统计图的一部分如图（其中分组情况见表）：
| 组别 |
范围（小时） |
| A |
 |
| B |
 |
| C |
 |
| D |
 |
请根据上述信息解答下列问题：
（1）B组的人数是人；
（2）本次调查数据（指体育活动时间）的中位数落在组内；
（3）若某地约有64000名中小学生，请你估计其中达到国家规定体育活动时间（不低于1小时）的人数约有多少?
如图，在平面直角坐标系中，已知抛物线y＝－
x2＋bx＋c经过点A(0，1)、B（3，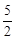
）两点，BC⊥x轴，垂足为C．点P是线段AB上的一动点（不与A，B重合），过点P作x轴的垂线交抛物线于点M，设点P的横坐标为t．
(1)求此抛物线的函数表达式；
(2)连结AM、BM，设△AMB的面积为S，求S关于t的函数关系式，并求出S的最大值；
(3)连结PC，当t为何值时，四边形PMBC是菱形．
已知关于x的方程(k-2)x2＋2(k-2)x＋k＋1=0有两个实数根，求正整数k的值．
已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．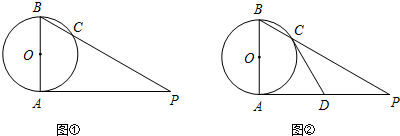
（1）如图①，若AB=2，∠P=30°，求AP的长（结果保留根号）；
（2）如图②，若D为AP的中点，求证直线CD是⊙O的切线．
小明所在班组织全部同学参加上海世博园，由于时间原因，每个学生只能在所给的场馆单（如图）上随机选择，选择方式规定为在3个发展中国家馆和4个发达国家馆中分别选一个馆参观。场馆单上的3个发展中国家馆包括：A中国馆、B印度馆、C巴西馆；4个发达国家馆包括：D美国馆、E日本馆、F德国馆、G法国馆，其中中国馆、印度馆、日本馆属于亚洲馆。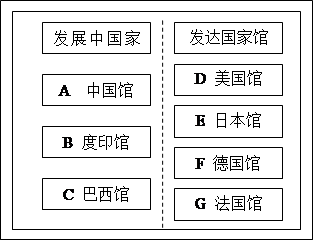
（1）请你用列表或画树状图的方法，分析并写出小明所有可能的参观方式。（馆名用字母表示即可）
（2）求小明所选择参观的两个馆恰好都是亚洲馆的概率。