将图中的A型（正方形）、B型（菱形）、C型（等腰直角三角形）-优题课

将图中的 $A$ 型（正方形）、 $B$ 型（菱形）、 $C$ 型（等腰直角三角形）纸片分别放在3个盒子中，盒子的形状、大小、质地都相同，再将这3个盒子装入一只不透明的袋子中．

（1）搅匀后从中摸出1个盒子，盒中的纸片既是轴对称图形又是中心对称图形的概率是　　；

（2）搅匀后先从中摸出1个盒子（不放回），再从余下的2个盒子中摸出1个盒子，把摸出的2个盒中的纸片长度相等的边拼在一起，求拼成的图形是轴对称图形的概率．（不重叠无缝隙拼接）

科目数学题型解答题难度中等

知识点：概率公式列表法与树状图法

某兴趣小组借助无人飞机航拍校园．如图，无人飞机从 A处水平飞行至 B处需8秒，在地面 C处同一方向上分别测得 A处的仰角为75°， B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）

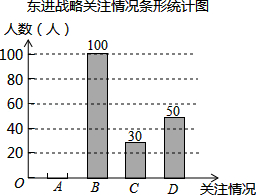
深圳市政府计划投资1.4万亿元实施东进战略．为了解深圳市民对东进战略的关注情况．某校数学兴趣小组随机采访部分深圳市民，对采访情况制作了统计图表的一部分如下：

（1）根据上述统计图可得此次采访的人数为　　人， m＝　　， n＝　　；

（2）根据以上信息补全条形统计图；

（3）根据上述采访结果，请估计在15000名深圳市民中，高度关注东进战略的深圳市民约有　　人．

解不等式组： $\{\begin{matrix} 5 x - 1 < 3 (x + 1) \\ \frac{2 x - 1}{3} - 1 \leq \frac{5 x + 1}{2} \end{matrix}$ ．

如图，点 C为△ ABD的外接圆上的一动点（点 C不在 $\hat{BAD}$ 上，且不与点 B， D重合），∠ ACB＝∠ ABD＝45°

（1）求证： BD是该外接圆的直径；

（2）连结 CD，求证： $\sqrt{2} AC = BC + CD$ ；

（3）若△ ABC关于直线 AB的对称图形为△ ABM，连接 DM，试探究 DM ²， AM ²， BM ²三者之间满足的等量关系，并证明你的结论．

已知抛物线 y＝ mx ²+（1﹣2 m） x+1﹣3 m与 x轴相交于不同的两点 A、 B

（1）求 m的取值范围；

（2）证明该抛物线一定经过非坐标轴上的一点 P，并求出点 P的坐标；

（3）当 $\frac{1}{4}$ ＜ m≤8时，由（2）求出的点 P和点 A， B构成的△ ABP的面积是否有最值？若有，求出该最值及相对应的 m值．