如图，ΔABC和ΔCDE都是等边三角形，点B、C、E三点在同-优题课

游客

题文

如图， $ΔABC$ 和 $ΔCDE$ 都是等边三角形，点 $B$ 、 $C$ 、 $E$ 三点在同一直线上，连接 $BD$ ， $AD$ ， $BD$ 交 $AC$ 于点 $F$ ．

（1）若 $A D^{2} = DF \cdot DB$ ，求证： $AD = BF$ ；

（2）若 $∠ BAD = 90 °$ ， $BE = 6$ ．

①求 $\tan ∠ DBE$ 的值；②求 $DF$ 的长．

科目数学题型解答题难度中等

知识点：解直角三角形相似三角形的判定与性质全等三角形的判定与性质等边三角形的性质

登录免费查看答案和解析

相关试题

如图，△ABC中，∠ACB=90°，AC=BC，点A、C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的二次函数图象经过点B、D．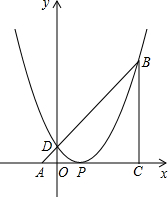

（1）用m的代数式表示点A、D的坐标；
（2）求这个二次函数关系式；
（3）点Q（x，y）为二次函数图象上点P至点B之间的一点，连接PQ、BQ，当x为何值时，四边形ABQP的面积最大？

某商店经销一种成本为每千克40元的产品，若按每千克50元销售，一个月能售出500千克. 销售单价每涨1元，月销售量就减少10千克，针对这种产品，请解答以下问题：
（1）当销售单价定为每千克55元时，计算销售量与月销售利润；
（2）商店想在销售额不超过20000元的情况下，使得月销售利润达到8000元，则销售单价应为多少？

已知一个三角形的两边长分别是３和４，第三边是方程的根
（1）判断这个三角形的形状；
（2）求这个三角形第三边上的高.

如图，一艘轮船从离A观察站的正北海里处的B港出发向东航行，观察站第一次测得该船在A地北偏东30°的C处；半小时后，又测得该船在A地的北偏东60°的D处，求此船的速度.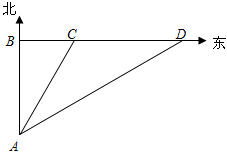

已知关于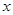的一元二次方程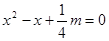有两个实数根，若m为正整数，求此方程的根．

试卷网试题网古诗词网作文网范文网