如图, 内接于 ,点 在 外, , 交 于点 ,交 于点 , , , , .
(1)求证: ;
(2)求证:
是
的切线;
(3)求 的值.
(年青海省西宁市)某校数学兴趣小组要测量西山植物园蒲宁之珠的高度.如图,他们在点A处测得蒲宁之珠最高点C的仰角为45°,再往蒲宁之珠方向前进至点B处测得最高点C的仰角为56°,AB=62m,根据这个兴趣小组测得的数据,则蒲宁之珠的高度CD约为 m.(sin56°≈0.83,tan56°≈1.49,结果保留整数)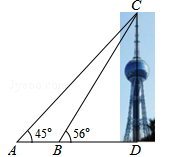
(年蒙自市初中学业水平第一次模拟测试)如图 ,
, ,
, ,求证:
,求证:

(年青海省中考)如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.
(1)求建筑物BC的高度;
(2)求旗杆AB的高度(结果精确到0.1米).
参考数据: ≈1.41,
≈1.41, ≈1.73.
≈1.73.
(年贵州省黔南州)如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=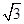 :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: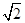 ≈1.414,
≈1.414,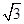 ≈1.732)
≈1.732)
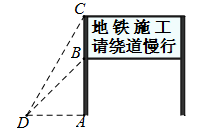
(年蒙自市初中学业水平第一次模拟测试)在某市地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如图所示).已知立杆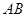 的高度是
的高度是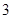 米,从路侧点
米,从路侧点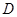 处测得路况警示牌顶端
处测得路况警示牌顶端 点和底端
点和底端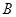 点的仰角分别是
点的仰角分别是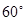 和
和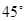 ,求路况警示牌宽
,求路况警示牌宽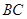 的值.(精确到0.1米)(参考数据:
的值.(精确到0.1米)(参考数据: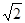 ≈1.41,
≈1.41,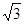 ≈1.73)
≈1.73)