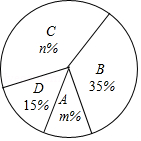
今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为 $A$， $B$， $C$， $D$四个等级，并绘制了如下不完整的频数分布表和扇形统计图：

等级	成绩 $\left(s\right)$	频数（人数）
$A$	$90<s⩽100$	4
$B$	$80<s⩽90$	$x$
$C$	$70<s⩽80$	16
$D$	$s⩽70$	6

根据以上信息，解答以下问题：

（1）表中的 $x=$　      　；

（2）扇形统计图中 $m=$　     　， $n=$　     　， $C$等级对应的扇形的圆心角为　         　度；

（3）该校准备从上述获得 $A$等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用 $a_1$， $a_2$表示）和两名女生（用 $b_1$， $b_2$表示），请用列表或画树状图的方法求恰好选取的是 $a_1$和 $b_1$的概率．

科目 数学   题型 解答题   难度 中等

知识点： 列表法与树状图法 频数（率）分布表 扇形统计图