某校为了推进学校均衡发展,计划再购进一批图书,丰富学生的课外阅读.为了解学生对课外阅读的需求情况,学校对学生所喜爱的读物:
.文学,
.艺术,
.科普,
.生活,
.其他,进行了随机抽样调查(规定每名学生只能选其中一类读物),并将调查结果绘制成以下不完整的统计图表.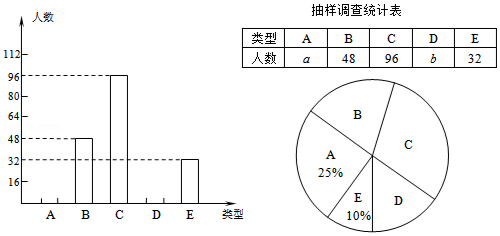
(1) , ,请补全条形统计图;
(2)如果全校有2500名学生,请你估计全校有多少名学生喜爱科普读物;
(3)学校从喜爱科普读物的学生中选拔出2名男生和3名女生,并从中随机抽取2名学生参加科普知识竞赛,请你用树状图或列表法求出恰好抽到一名男生和一名女生的概率.
据媒体报道,我国2010年公民出境旅游总人数约5000万人次,2012年公民出境旅游总人数约7200万人次,若2011年、2012年公民出境旅游总人数逐年递增,请解答下列问题:
(1)求这两年我国公民出境旅游总人数的年平均增长率;
(2)如果2012年仍保持相同的年平均增长率,请你预测2013年我国公民出境旅游总人数约多少万人次?
如图,西园中学数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点 的仰角为
的仰角为 ,再沿着
,再沿着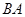 的方向后退20m至
的方向后退20m至 处,测得古塔顶端点
处,测得古塔顶端点 的仰角为
的仰角为 ,求该古塔BD的高度(
,求该古塔BD的高度(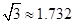 ,结果保留一位小数).
,结果保留一位小数).
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).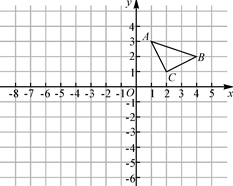
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使 =
=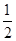 ,并写出点A2的坐标。
,并写出点A2的坐标。
如图,在△ABC中,AB=AC=10cm,BD⊥AC于D,且BD=8cm.点M从点A出发,沿AC方向匀速运动,速度为2cm/s;同时直线PQ由点B出发沿BA方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于P,交BC于Q,连接PM,设运动时间为t(s)(0<t<5).
(1)当四边形PQCM是平行四边形时,求t的值;
(2)当t为何值时,△PQM是等腰三角形?
(3)以PM为直径作⊙E,在点P、Q整个运动过程中,是否存在这样的时刻t,使得⊙E与BC相切?若存在,请求出运动时间t的值;若不存在,请说明理由.
如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.
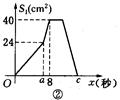

(1)参照图象,求b、图②中c及d的值;
(2)连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为;
(3)当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)若点P、点Q在运动路线上相距的路程为25cm,求x的值.