为了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘成如图所示的频数分布直方图,已知成绩 (单位:分)均满足“ ”.根据图中信息回答下列问题:
(1)图中 的值为 ;
(2)若要绘制该样本的扇形统计图,则成绩 在“ ”所对应扇形的圆心角度数为 度;
(3)此次比赛共有300名学生参加,若将“ ”的成绩记为“优秀”,则获得“优秀“的学生大约有 人:
(4)在这些抽查的样本中,小明的成绩为92分,若从成绩在“ ”和“ ”的学生中任选2人,请用列表或画树状图的方法,求小明被选中的概率.

计算:
先化简,再求值: ,其中 满足 .
解不等式组,并将解集在数轴上表示出来.
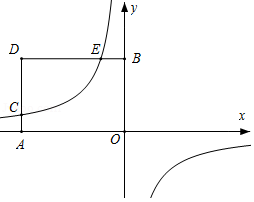
如图,在平面直角坐标系中,矩形 的顶点 , 的坐标分别为 , .过点 的双曲线 与矩形 的边 交于点 .
(1)填空: , ,点 的坐标为 ;
(2)当 时,经过点 与点 的直线交 轴于点 ,点 是过 , 两点的抛物线 的顶点.
①当点 在双曲线 上时,求证:直线 与双曲线 没有公共点;
②当抛物线 与矩形 有且只有三个公共点,求 的值;
③当点 和点 随着 的变化同时向上运动时,求 的取值范围,并求在运动过程中直线 在四边形 中扫过的面积.
某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为 ,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的 值都以平均值 计算.第一年有40家工厂用乙方案治理,共使 值降低了12.经过三年治理,境内长江水质明显改善.
(1)求 的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数 ,三年来用乙方案治理的工厂数量共190家,求 的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的 值比上一年都增加一个相同的数值 .在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的 值与当年用甲方案治理降低的 值相等,第三年,用甲方案使 值降低了39.5.求第一年用甲方案治理降低的 值及 的值.