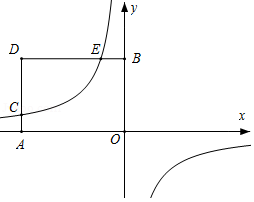
如图,在平面直角坐标系中,矩形 的顶点 , 的坐标分别为 , .过点 的双曲线 与矩形 的边 交于点 .
(1)填空: , ,点 的坐标为 ;
(2)当 时,经过点 与点 的直线交 轴于点 ,点 是过 , 两点的抛物线 的顶点.
①当点 在双曲线 上时,求证:直线 与双曲线 没有公共点;
②当抛物线 与矩形 有且只有三个公共点,求 的值;
③当点 和点 随着 的变化同时向上运动时,求 的取值范围,并求在运动过程中直线 在四边形 中扫过的面积.
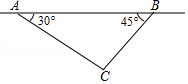
如图所示,飞机在一定高度上沿水平直线飞行,先在点 处测得正前方小岛 的俯角为 ,面向小岛方向继续飞行 到达 处,发现小岛在其正后方,此时测得小岛的俯角为 ,如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
先化简,再求值: ,其中 .
计算: .
如图,二次函数 的图象与 轴交于 、 两点,与 轴交于点 , .点 在函数图象上, 轴,且 ,直线 是抛物线的对称轴, 是抛物线的顶点.
(1)求 、 的值;
(2)如图①,连接 ,线段 上的点 关于直线 的对称点 恰好在线段 上,求点 的坐标;
(3)如图②,动点 在线段 上,过点 作 轴的垂线分别与 交于点 ,与抛物线交于点 .试问:抛物线上是否存在点 ,使得 与 的面积相等,且线段 的长度最小?如果存在,求出点 的坐标;如果不存在,说明理由.

某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点 出发,在矩形 边上沿着 的方向匀速移动,到达点 时停止移动.已知机器人的速度为1个单位长度 ,移动至拐角处调整方向需要 (即在 、 处拐弯时分别用时 ).设机器人所用时间为 时,其所在位置用点 表示, 到对角线 的距离(即垂线段 的长)为 个单位长度,其中 与 的函数图象如图②所示.
(1)求 、 的长;
(2)如图②,点 、 分别在线段 、 上,线段 平行于横轴, 、 的横坐标分别为 、 .设机器人用了 到达点 处,用了 到达点 处(见图①).若 ,求 、 的值.
