我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将 化为分数形式
由于 ,设 ①
则 ②
② ①得 ,解得 ,于是得 .
同理可得 ,
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(基础训练)
(1) , ;
(2)将 化为分数形式,写出推导过程;
(能力提升)
(3) , ;
(注 ,
(探索发现)
(4)①试比较 与1的大小: 1(填“ ”、“ ”或“ ”
②若已知 ,则 .
(注
如图,在直角坐标系 中,菱形 的边 在 轴正半轴上,点 , 在第一象限, ,边长 .点 从原点 出发沿 轴正半轴以每秒1个单位长的速度作匀速运动,点 从 出发沿边 以每秒2个单位长的速度作匀速运动,过点 作直线 垂直于 轴并交折线 于 ,交对角线 于 ,点 和点 同时出发,分别沿各自路线运动,点 运动到原点 时, 和 两点同时停止运动.
(1)当 时,求线段 的长;
(2)求 为何值时,点 与 重合;
(3)设 的面积为 ,求 与 的函数关系式及 的取值范围.

我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量 (万件)与月份 (月)的关系为: ,每件产品的利润 (元)与月份 (月)的关系如下表:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
10 |
10 |
(1)请你根据表格求出每件产品利润 (元)与月份 (月)的关系式;
(2)若月利润 (万元) 当月销售量 (万件) 当月每件产品的利润 (元),求月利润 (万元)与月份 (月)的关系式;
(3)当 为何值时,月利润 有最大值,最大值为多少?
已知直线 与抛物线 .
(1)求证:直线 与该抛物线总有两个交点;
(2)设直线 与该抛物线两交点为 , , 为原点,当 时,求 的面积.
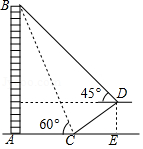
如图,在大楼 正前方有一斜坡 ,坡角 ,楼高 米,在斜坡下的点 处测得楼顶 的仰角为 ,在斜坡上的 处测得楼顶 的仰角为 ,其中点 , , 在同一直线上.
(1)求坡底 点到大楼距离 的值;
(2)求斜坡 的长度.
如图,反比例函数 过点 ,直线 与 轴交于点 ,过点 作 轴的垂线 交反比例函数图象于点 .
(1)求 的值与 点的坐标;
(2)在平面内有点 ,使得以 , , , 四点为顶点的四边形为平行四边形,试写出符合条件的所有 点的坐标.
