如图1,在平面直角坐标系中,直线 分别与 轴、 轴交于点 , , ,等边 的顶点 与原点 重合, 边落在 轴正半轴上,点 恰好落在线段 上,将等边 从图1的位置沿 轴正方向以每秒1个单位长度的速度平移,边 , 分别与线段 交于点 , (如图2所示),设 平移的时间为 .
(1)等边 的边长为 ;
(2)在运动过程中,当 时, 垂直平分 ;
(3)若在 开始平移的同时.点 从 的顶点 出发.以每秒2个单位长度的速度沿折线 运动.当点 运动到 时即停止运动. 也随之停止平移.
①当点 在线段 上运动时,若 与 相似.求 的值;
②当点 在线段 上运动时,设 ,求 与 的函数关系式,并求出 的最大值及此时点 的坐标.

在数轴上表示下列各数,并按从小到大的顺序用“<”号连接起来. , +3 , 0 ,
, +3 , 0 ,  , -
, -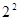 ,
, 

计算下列各题:(每小题5分,共25分)
(1)(+45)+(-92)+35+(-8) (2)(1-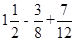 )×(-24)
)×(-24)
(3)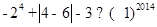 (4)化简:3ab-
(4)化简:3ab- -2ba-3
-2ba-3
(5)先化简后求值: ,其中
,其中 .
.
解方程组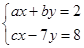 时,本应解出
时,本应解出
 ,由于看错了系数
,由于看错了系数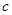 ,而得出解
,而得出解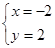 ,求
,求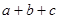 的值。
的值。
已知:如图AD∥BE,∠1=∠2,试说明:∠A=∠E.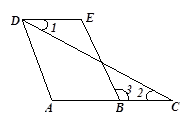
(1)如图(1)∠AOB和∠COD都是直角,请你指出∠AOD和∠BOC之间的数量关系;
(2)当∠COD绕点O旋转到如图(2)所示的位置时,上述结论还成立吗?请说明理由.
(3)如图(3),当∠AOB=∠COD=β(0°<β<90°)时,请你直接写出∠AOD和∠BOC之间的数量关系(不用说明理由).