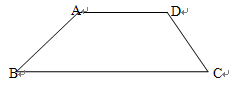
在线段 的同侧作射线 和 ,若 与 的平分线分别交射线 , 于点 , , 和 交于点 .如图,点点同学发现当射线 , 交于点 ;且 时,有以下两个结论:
① ;② .
那么,当 时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出 的度数,写出 , , 长度之间的等量关系,并给予证明;
(2)设点 为线段 上一点, ,若 ,四边形 的面积为 ,求 的长.
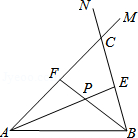
已知:正方形ABCD中,DM=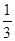 CM,AN⊥BM于N,求:cos∠NAD的值
CM,AN⊥BM于N,求:cos∠NAD的值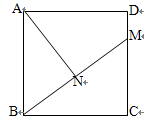
已知:二次函数y=x2-3x-2与y=-2x+4交于点A、B(点A在点B的左边),(1) 求点A、B的坐标;
(2) 请根据图象判断x2-3x-2≤-2x+4的解集。
已知抛物线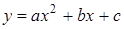 经过点
经过点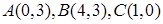 .
.(1) 求该抛物线的解析式;
(2) 当y随x的增大而增大时,x的取值范围是什么?
已知二次函数y= x2 +4x+3.(1)求二次函数图象与x轴的交点A、B(A在B的左侧)及顶点的坐标;
(2)在平面直角坐标系中,画出这个二次函数的图象;
(3)写出当x为何值时,y>0.
已知:如图在梯形ABCD中,AD//BC,∠ABC=45o,∠ADC=120o,AD=DC,AB=2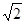 ,求:BC的长。
,求:BC的长。