课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为 ,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为 时,透光面积最大值约为 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为 ,利用图3,解答下列问题:
(1)若 为 ,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.

解不等式组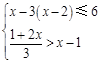 .
.
如图,已知直线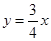 ,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线
,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线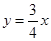 上的一点,以点A、B、D为顶点作正方形.
上的一点,以点A、B、D为顶点作正方形.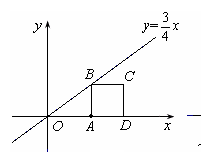
(1)若图仅看作符合条件的一种情况,求出所有符合条件的点D的坐标;
(2)在图中,若点P以每秒1个单位长度的速度沿直线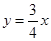 从点O移动到点B,与此同时点Q以相同的速度从点A出发沿着折线A-B-C移动,当点P到达点B时两点停止运动.试探究:在移动过程中,△PAQ的面积最大值是多少?
从点O移动到点B,与此同时点Q以相同的速度从点A出发沿着折线A-B-C移动,当点P到达点B时两点停止运动.试探究:在移动过程中,△PAQ的面积最大值是多少?
已知矩形纸片ABCD中,AB=2,BC=3.
操作:将矩形纸片沿EF折叠,使点B落在边CD上.
探究:
(1)如图1,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等,请给出证明,如果不全等,请说明理由;
(2)如图2,若点B与CD的中点重合,请你判断△FCB1、△B1DG和△EA1G之间的关系,如果全等,只需写出结果,如果相似,请写出结果和相应的相似比;
(3)如图2,请你探索,当点B落在CD边上何处,即B1C的长度为多少时,△FCB1与△B1DG全等.
在直角三角形ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧BC相切于点D,交AC于点E,连接AD.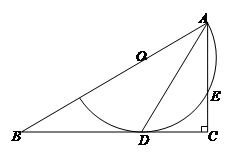
(1)求证:AD平分∠BAC;
(2)已知AE=2,DC=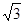 ,求圆弧的半径.
,求圆弧的半径.
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37º,∠CBE=45º,CD=1.3m,AB、CD之间的距离为5.1m.求AD、AB的长.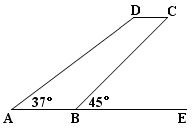
(参考数据: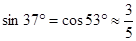 ,
,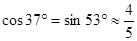 ,
,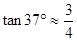 )
)