如图,过抛物线 上一点 作 轴的平行线,交抛物线于另一点 ,交 轴于点 ,已知点 的横坐标为 .
(1)求抛物线的对称轴和点 的坐标;
(2)在 上任取一点 ,连接 ,作点 关于直线 的对称点 ;
①连接 ,求 的最小值;
②当点 落在抛物线的对称轴上,且在 轴上方时,求直线 的函数表达式.

如下图是由三个小正方形组成的“L”形图,请你用三种方法分别在图中添加一个小正方形使它成为轴对称图形。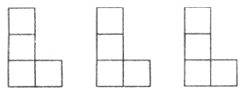
已知:直角梯形 中,
中, ∥
∥ ,∠
,∠ =
= ,以
,以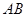 为直径的圆
为直径的圆 交
交 于点
于点 、
、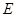 ,连结
,连结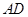 、
、 、
、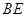 .
.
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形:
_____________________,______________________ ;
(2)直角梯形 中,以
中,以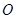 为坐标原点,
为坐标原点, 在
在 轴正半轴上建立直角坐标系(如图2),若抛物线
轴正半轴上建立直角坐标系(如图2),若抛物线 经过点
经过点 、
、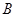 、
、 ,且
,且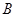 为抛物线的顶点.
为抛物线的顶点.
①写出顶点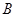 的坐标(用含
的坐标(用含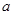 的代数式表示)___________;
的代数式表示)___________;
②求抛物线的解析式;
③在 轴下方的抛物线上是否存在这样的点
轴下方的抛物线上是否存在这样的点 ,过点
,过点 作
作 ⊥
⊥ 轴于点
轴于点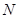 ,使得以点
,使得以点 、
、 、
、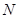 为顶点的三角形与△
为顶点的三角形与△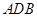 相似?若存在,求出点
相似?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
如图,已知 ,
, 两点的坐标分别为(
两点的坐标分别为( ,
, ),(
),( ,
, ),⊙
),⊙ 的圆心坐标为(
的圆心坐标为( ,
, ),并与
),并与 轴交于坐标原点
轴交于坐标原点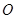 .若
.若 是⊙
是⊙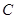 上的一个动点,线段
上的一个动点,线段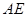 与
与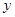 轴交于点
轴交于点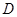 .
.
(1)线段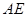 长度的最小值是_________,最大值是_________;
长度的最小值是_________,最大值是_________;
(2)当点 运动到点
运动到点 和点
和点 时,线段
时,线段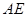 所在的直线与⊙
所在的直线与⊙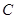 相切,求由
相切,求由
 、
、
 、弧
、弧
 所围成的图形的面积;
所围成的图形的面积;
(3)求出△ 的最大值和最小值
的最大值和最小值
阅读材料,解答问题.
例如图,在△ 中,∠
中,∠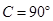 ,∠
,∠ ,利用此等腰直角三角形你能求出
,利用此等腰直角三角形你能求出 的值吗?
的值吗?
解:延长 到点
到点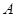 ,使
,使 ,连结
,连结 .
.
设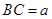 (
( ).
).
∵在△ 中,∠
中,∠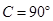 ,∠
,∠ .
.
∴∠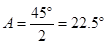 .
.
∴ ,
, .
.
∴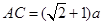 .
.
∴ .
.
(1)仿照上例,求出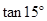 的值;
的值;
(2)在一次课外活动中,小刘从上例得到启发,用硬纸片做了两个直角三角形,如图1、图2.图1中,∠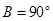 ,∠
,∠ ,
,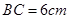 ;图2中,∠
;图2中,∠ ,∠
,∠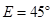 ,
, .图3是小刘所做的一个实验:他将△
.图3是小刘所做的一个实验:他将△ 的直角边
的直角边 与△
与△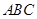 的斜边
的斜边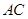 重合在一起,并将△
重合在一起,并将△ 沿
沿 方向移动.在移动过程中,
方向移动.在移动过程中,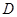 、
、 两点始终在
两点始终在 边上(移动开始时点
边上(移动开始时点 与点
与点 重合).
重合).
①在△ 沿
沿 方向移动的过程中,∠
方向移动的过程中,∠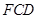 的度数逐渐__________.(填“不变”、“变大”、“变小”)
的度数逐渐__________.(填“不变”、“变大”、“变小”)
②在△ 移动过程中,是否存在某个位置,使得∠
移动过程中,是否存在某个位置,使得∠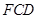
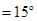 ?如果存在,求出
?如果存在,求出 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日均销售量的关系如下表:
| 销售单价(元) |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 日均销售量(瓶) |
480 |
440 |
400 |
360 |
320 |
280 |
240 |
(1)若记销售单价比每瓶进价多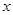 元时,日均毛利润(毛利润=售价
元时,日均毛利润(毛利润=售价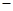 进价
进价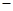 固定成本)为
固定成本)为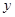 元,求
元,求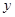 关于
关于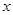 的函数解析式和自变量的取值范围;
的函数解析式和自变量的取值范围;
(2)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?