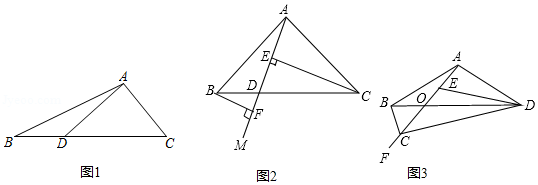
我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)概念理解:
如图1,在 中, , , ,试判断 是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2, 是“等高底”三角形, 是”等底”,作 关于 所在直线的对称图形得到△ ,连接 交直线 于点 .若点 是△ 的重心,求 的值.
(3)应用拓展:
如图3,已知 , 与 之间的距离为2.“等高底” 的“等底” 在直线 上,点 在直线 上,有一边的长是 的 倍.将 绕点 按顺时针方向旋转 得到△ , 所在直线交 于点 .求 的值.
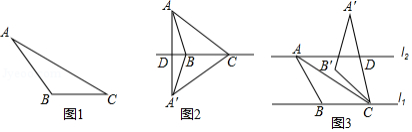
如图, 地在 地的北偏东 方向上, 地在 地的北偏西 方向上,原来从 地到 地的路线为 ,现在沿 地北偏东 方向新修了一条直达 地的分路,路程比原来少了20千米.求从 地直达 地的路程(结果保留整数.参考数据: ,
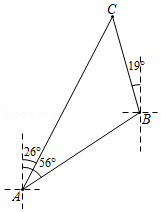
如图, 内接于圆 ,且 ,延长 到点 ,使 ,连接 交圆 于点 .
(1)求证: ;
(2)填空:
①当 的度数为 时,四边形 是菱形.
②若 , ,则 的长为 .
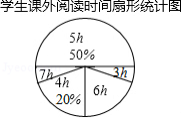
某中学为培养学生的阅读习惯,开展了"读书周"活动,并随机调查了该校部分学生这一周的课外阅读时间,将结果绘制成了如下尚不完整的统计图表
学生课外阅读时间统计表
|
阅读时间 |
频数 |
|
3 |
3 |
|
4 |
|
|
5 |
30 |
|
6 |
12 |
|
7 |
3 |
请你根据以上信息回答下列问题
(1)填空: ,本次调查的人数为 ;
(2)本次调查中,学生阅读时间的中位数为 ;
(3)扇形统计图中,课外阅读 所对应的圆心角的度数是 ;
(4)根据调查数据,发现这一周的人均阅读时间比活动前增加了 ,求活动前的人均阅读时间.
如图1,过点 的抛物线 与直线 交于点 .点 是线段 上一动点,过点 作 轴的垂线,垂足为点 ,交抛物线于点 .设 的面积为 ,点 的横坐标为 .
(1)请直接写出 的值及抛物线的解析式.
(2)为探究 最大时点 的位置,甲、乙两同学结合图形给出如下解析:
甲:借助 的长与三角形面积公式,求出 关于 的函数关系式,可确定点 的位置.
乙:当点 运动到点 或点 时, 的值可看作0,则当点 运动到 中点时, 最大,即 最大时,点 为 的中点.
请参考甲的方法求出 最大时点 的坐标,进而判断乙的猜想是否正确,并说明理由.
(3)拓展探究:如图2,直线 与任意抛物线相交于 、 两点, 是线段 上的一个动点,过点 作抛物线对称轴的平行线,交该抛物线于点 .当 的面积最大时,点 一定是线段 的中点吗?试作出判断并说明理由.

(1)探索发现
如图1,在 中,点 在边 上, 与 的面积分别记为 与 ,试判断 与 的数量关系,并说明理由.
(2)阅读解析
小东遇到这样一个问题:如图2,在 中, , ,射线 交 于点 ,点 、 在 上,且 ,试判断 、 、 三条线段之间的数量关系.
小东利用一对全等三角形,经过推理使问题得以解决.
填空:①图2中的一对全等三角形为 ;
② 、 、 三条线段之间的数量关系为 .
(3)类比探究
如图3,在四边形 中, , 与 交于点 ,点 、 在射线 上,且 .
①判断 、 、 三条线段之间的数量关系,并说明理由;
②若 , 的面积为2,直接写出四边形 的面积.