如图，公交车行驶在笔直的公路上，这条路上有 ， ， ， 四个站点，每相邻两站之间的距离为5千米，从 站开往 站的车称为上行车，从 站开往 站的车称为下行车，第一班上行车、下行车分别从 站、 站同时发车，相向而行，且以后上行车、下行车每隔10分钟分别在 ， 站同时发一班车，乘客只能到站点上、下车（上、下车的时间忽略不计），上行车、下行车的速度均为30千米 小时．
（1）问第一班上行车到 站、第一班下行车到 站分别用时多少？
（2）若第一班上行车行驶时间为 小时，第一班上行车与第一班下行车之间的距离为 千米，求 与 的函数关系式；
（3）一乘客前往 站办事，他在 ， 两站间的 处（不含 ， 站），刚好遇到上行车， 千米，此时，接到通知，必须在35分钟内赶到，他可选择走到 站或走到 站乘下行车前往 站．若乘客的步行速度是5千米 小时，求 满足的条件．
(本题5分)如图，已知AD∥BC，∠1=∠2，说明∠3+∠4=180°，请完成说明过程，并在括号内填上相应依据：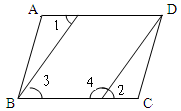
解：∠3+∠4=180°，理由如下：
∵AD∥BC（已知），
∴∠1=∠3（）
∵∠1=∠2（已知）
∴∠2=∠3（等量代换）；
∴∥（）
∴∠3+∠4=180°（）
解下列不等式（组），并将其解集在数轴上表示出来。
（1）
＜
+1(2)
（1）已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h
└─────┘a└──────┘h
(2)如图，已知△ABC，请作出△ABC关于X轴对称的图形．并写出A、B、C 关于x轴对称的点坐标。
在边长为6的菱形ABCD中，动点M从点A出发，沿A→B→C向终点C运动，连接DM交AC于点N．
（1）如图1，当点M在AB边上时，连接BN
①试说明：
；
②若∠ABC=60°，AM=4，求点M到AD的距离．
（2）如图2，若∠ABC=90°，记点M运动所经过的路程为x（6≤x≤12）．试问：x为何值时，△ADN为等腰三角形．
如图所示，四边形OABC是矩形，点D在OC边上，以AD为折痕，将△OAD向上翻折，点O恰好落在BC边上的点E处，若△ECD的周长为2，△EBA的周长为6．
（1）矩形OABC的周长为；
（2）若A点坐标为
，求线段AE所在直线的解析式．