某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚,到了收获季节,已知该蜜柚的成本价为8元 千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量 (千克)与销售单价 (元 千克)之间的函数关系如图所示.
(1)求 与 的函数关系式,并写出 的取值范围;
(2)当该品种的蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.

解不等式 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
解方程:
(a)100×100=1002=10000,
(b)99×101=1002-1=9999,
(c)98×102=-=,
(d)97×=-=.
(1)用含有n的式子表示上述规律_________;
(2)上述式子左边两因数的和总是200,而积却因两因数的接近程度而不同,两因数越接近,其积就越;而当两因数时,其积最大,最大值为.
(3)已知a+b=100,则ab的最大值为;
(4)用10米长的绳子围成一个矩形,怎样才能使矩形面积最大?最大的面积是多少?
观察并填空:如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点D、C,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.
(1)探究∠1、∠2、∠3之间的关系,并说明你的结论的正确性.
(2)若点P在A、B两点之间运动时(点P和A、B不重合),∠1、∠2、∠3之间的关系发生变化(填“会”或“不会”);
(3)如果点P在A、B两点外侧运动时,(点P和A、B不重合)
①当点P在射线AM上时,猜想∠1、∠2、∠3之间的关系为;
②当点P在射线BN上时,猜想∠1、∠2、∠3之间的关系为(不必证明).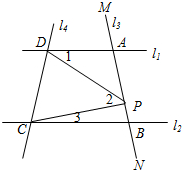
如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
(1)此变化过程中,是自变量,是因变量;
(2)甲的速度乙的速度(大于、等于、小于);
(3)6时表示;
(4)路程为150km,甲行驶了小时,乙行驶了小时;
(5)9时甲在乙的(前面、后面、相同位置);
(6)乙比甲先走了3小时,对吗?.