将图中的 型、 型、 型矩形纸片分别放在3个盒子中，盒子的形状、大小、质地都相同，再将这3个盒子装入一只不透明的袋子中．
（1）搅匀后从中摸出1个盒子，求摸出的盒子中是 型矩形纸片的概率；
（2）搅匀后先从中摸出1个盒子（不放回），再从余下的两个盒子中摸出一个盒子，求2次摸出的盒子的纸片能拼成一个新矩形的概率（不重叠无缝隙拼接）．
（本题5分）若新规定这样一种运算法则：a※b=a2+2ab，
例如3※（-2）=32+2×3×（-2）=－3
（1）试求（－2）※3的值
（2）若（－2）※x=－2+ x , 求x的值
解方程：
⑴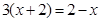
；
⑵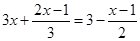
．
化简，求值
已知
，求
的值．
（本题10分）在弹性程度内，一根弹簧最大可伸长长度为58 cm．如图是由三根相同的上述弹簧构成的拉力器，已知拉力y与弹簧的总长度x之间是一次函数的关系，函数y与自变量x的部分对应值如下表：
| x（单位：cm） |
28 |
30 |
35 |
| y（单位：N） |
0 |
120 |
420 |
（1）求y与x之间的函数关系式，并写出自变量x的取值范围；
（2）求拉力y的最大值；
（3）已知某儿童最大拉力为400N，求该儿童能使单根弹簧伸长的最大长度．
（本题9分）如图，直线y＝－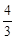
x＋8与x轴、y轴分别相交于点A、B，设M是OB上一点，
若将△ABM沿AM折叠，使点B恰好落在x轴上的点B'处．求：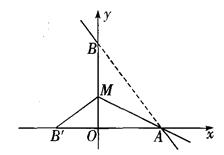
（1）点B'的坐标:．
（2）直线AM所对应的函数关系式．