某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调查.获取信息如下:
购买数量低于5000块 |
购买数量不低于5000块 |
|
红色地砖 |
原价销售 |
以八折销售 |
蓝色地砖 |
原价销售 |
以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.
已知抛物线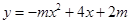 与x轴交于点A(α,0),B(β,0),且
与x轴交于点A(α,0),B(β,0),且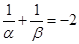 ,
,
(1)求抛物线的解析式.
(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E,是否存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.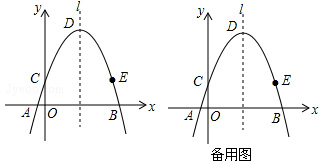
(本小题满分13分)
在平面直角坐标系中,O为原点,直线y =-2x-1与y轴交于点A,与直线y =-x交于点B, 点B关于原点的对称点为点C.
(1)求过A,B,C三点的抛物线的解析式;
(2)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②若点P的横坐标为t(-1<t<1),当t为何值时,四边形PBQC面积最大,并说明理由.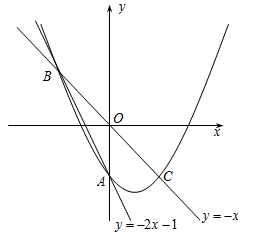
(1)请补全以下求不等式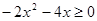 的解集的过程.
的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数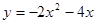 ;并在下面的坐标系中(见图1)画出二次函数
;并在下面的坐标系中(见图1)画出二次函数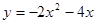 的图象(只画出图象即可).
的图象(只画出图象即可).
②求得界点,标示所需:当y=0时,求得方程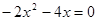 的解为 ;并用锯齿线标示出函数
的解为 ;并用锯齿线标示出函数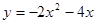 图象中y≥0的部分.
图象中y≥0的部分.
③借助图象,写出解集:由所标示图象,可得不等式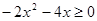 的解集为 .
的解集为 .
(2)利用(1)中求不等式解集的步骤,求不等式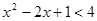 的解集.
的解集.
①构造函数,画出图象:
②求得界点,标示所需:
③借助图像,写出解集:
(3)参照以上两个求不等式解集的过程,借助一元二次方程的求根公式,直接写出关于x的不等式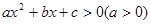 的解集.
的解集.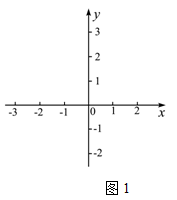
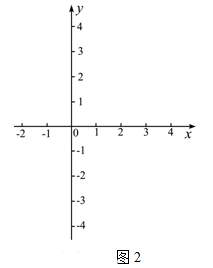
如图,在平面直角坐标系中,已知抛物线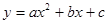 交
交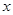 轴于
轴于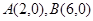 两点,交
两点,交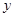 轴于点
轴于点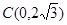 .
.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线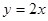 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交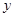 轴于点E、F两点,求劣弧
轴于点E、F两点,求劣弧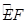 的长;
的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于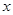 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.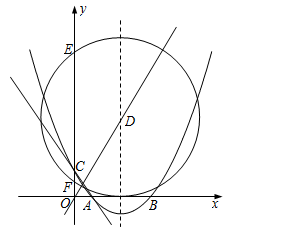
(本小题满分10分)
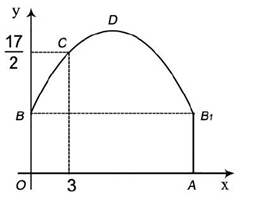
如图隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用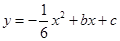 表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为
表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为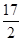 m。
m。
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?